题目内容
已知 、
、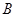 两盒中都有红球、白球,且球的形状、大小都相同,盒子
两盒中都有红球、白球,且球的形状、大小都相同,盒子 中有
中有 个红球与
个红球与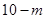 个白球,盒子
个白球,盒子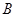 中有
中有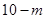 个红球与
个红球与 个白球(
个白球(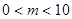 ).
).
(1)分别从 、
、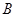 中各取一个球,
中各取一个球, 表示红球的个数;
表示红球的个数;
①请写出随机变量 的分布列,并证明
的分布列,并证明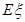 等于定值;
等于定值;
②当 为何值时,
为何值时,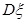 取到最小值,并求出最小值.
取到最小值,并求出最小值.
(2)在盒子 中不放回地摸取3个球,事件
中不放回地摸取3个球,事件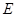 :在第一次取到红球后,以后两次都取到白球,事件
:在第一次取到红球后,以后两次都取到白球,事件 :在第一次取到白球后,以后两次都取到红球,若概率
:在第一次取到白球后,以后两次都取到红球,若概率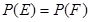 ,求
,求 的值.
的值.
(1)①见解析 ② (2)5
(2)5
解析试题分析:(1)①先确定 的取值,再分别求出
的取值,再分别求出 等于0、1、2时的概率,然后即可列表,确定
等于0、1、2时的概率,然后即可列表,确定 为定值②将值带入公式求解即可.(2)先求出事件E和F的概率表达式为
为定值②将值带入公式求解即可.(2)先求出事件E和F的概率表达式为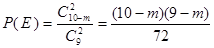 ;
;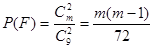 ,然后根据两式相等,即可求出m的值.
,然后根据两式相等,即可求出m的值.
试题解析:(1)① 的可能取值为0,1,2 1分
的可能取值为0,1,2 1分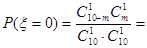
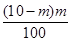
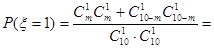
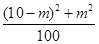
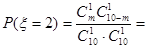
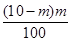 4分
4分
∴ 分布列为:
分布列为:
0 1 2 
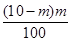
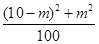
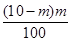

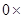
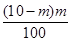
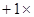
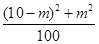

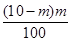
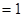 为定值 6分
为定值 6分
②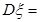
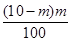
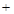
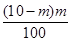
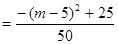 7分
7分 ,
,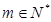 ,当
,当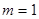 或
或 时,
时,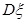 最小,最小值为
最小,最小值为 . 9分
. 9分
(2)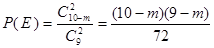 ,
,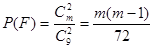 11分
11分
∵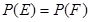 ∴
∴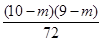
 ∴
∴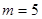 14分
14分
考点:1,离散型随机变量及其分布2,数学期望3,概率公式的应用.

练习册系列答案
相关题目
小王经营一家面包店,每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元,若当天卖不完,则未卖出的现烤面包因过期每个亏损5元.经统计,得到在某月(30天)中,小王每天售出的现烤面包个数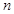 及天数如下表:
及天数如下表:
售出个数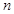 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天数 | 3 | 3 | 3 | 6 | 9 | 6 |
(1)计算小王某天售出该现烤面包超过13个的概率;
(2)若在今后的连续5天中,售出该现烤面包超过13个的天数大于3天,则小王决定增加订购量.试求小王增加订购量的概率.
(3)若小王每天订购14个该现烤面包,求其一天出售该现烤面包所获利润的分布列和数学期望.
我国政府对PM2.5采用如下标准:
| PM2.5日均值m(微克/立方米) | 空气质量等级 |
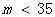 | 一级 |
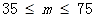 | 二级 |
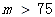 | 超标 |
某市环保局从180天的市区PM2.5监测数据中,随机抽取l0天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).

(1)求这10天数据的中位数.
(2)从这l0天的数据中任取3天的数据,记
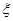 表示空气质量达到一级的天数,求
表示空气质量达到一级的天数,求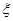 的分布列;
的分布列;(3)以这10天的PM2.5日均值来估计这180天的空气质量情况,其中大约有多少天的空气质量达到一级.
 .已知比赛中,乙先赢了第一局,求:
.已知比赛中,乙先赢了第一局,求: 为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为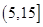 ,
,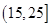 ,
,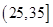 ,
,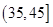 ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图.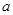 的值;
的值; 组的频率为
组的频率为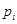 ,第
,第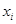
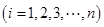 ,则样本数据的平均值为
,则样本数据的平均值为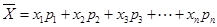 .)
.) ,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取
,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取 天的数值,其中达到“特优等级”的天数为
天的数值,其中达到“特优等级”的天数为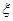 ,求
,求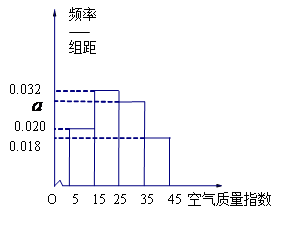
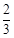 ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.(12分)
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.(12分)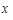 的分布列和数学期望.
的分布列和数学期望. 棵,梧桐树
棵,梧桐树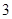 棵.它们移栽后的成活率分别
棵.它们移栽后的成活率分别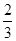 、
、 ,每棵树是否存活互不影响,在移栽的
,每棵树是否存活互不影响,在移栽的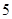 棵树中:
棵树中: 的分布列与期望.
的分布列与期望.