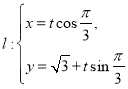题目内容
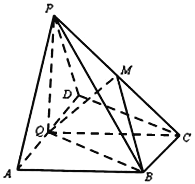
【题目】如图,公园内有一块边长为![]() 的正三角形
的正三角形![]() 空地,拟改建成花园,并在其中建一直道
空地,拟改建成花园,并在其中建一直道![]() 方便花园管理. 设
方便花园管理. 设![]() 分别在
分别在![]() 上,且
上,且![]() 均分三角形
均分三角形![]() 的面积.
的面积.
(1)设![]() (
(![]() ),
),![]() ,试将
,试将![]() 表示为
表示为![]() 的函数关系式;
的函数关系式;
(2)若![]() 是灌溉水管,为节约成本,希望其最短,
是灌溉水管,为节约成本,希望其最短,![]() 的位置应在哪里?若
的位置应在哪里?若![]() 是参观路线,希望其最长,
是参观路线,希望其最长,![]() 的位置应在哪里?
的位置应在哪里?

【答案】(1)![]() ;(2)当取
;(2)当取![]() 且
且![]() 时,
时,![]() 最短;当
最短;当![]() 与
与![]() 重合且
重合且![]() 为
为![]() 中点,或
中点,或![]() 与
与![]() 重合且
重合且![]() 为
为![]() 中点时,
中点时,![]() 最长
最长
【解析】
(1)根据![]() 均分三角形
均分三角形![]() 的面积可得
的面积可得![]() ,即得
,即得![]() ,再由余弦定理可得表达式;(2)令
,再由余弦定理可得表达式;(2)令![]() ,设
,设![]() ,用定义讨论函数单调性,求得
,用定义讨论函数单调性,求得![]() 的最大值和最小值,再由(1)中得到的关系式,可得
的最大值和最小值,再由(1)中得到的关系式,可得![]() 的最大值和最小值.
的最大值和最小值.
(1)![]() 均分三角形
均分三角形![]() 的面积,
的面积,![]() ,
,![]() ,即
,即![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
因为![]() ,所以
,所以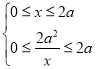 解得
解得![]() ,
,
故![]() 关于
关于![]() 的函数关系式为
的函数关系式为![]() .
.
(2)由(1),令![]() ,则
,则![]() ,且
,且![]() .设
.设![]() .
.
若![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上是减函数. 同理可得
上是减函数. 同理可得![]() 在
在![]() 上是增函数.
上是增函数.
于是当![]() 即
即![]() 时,代入解得:
时,代入解得:![]() ,此时
,此时![]() ,且
,且![]() ,
,
当![]() 或
或![]() 即
即![]() 或
或![]() 时,代入解得:
时,代入解得:![]() ,此时
,此时![]() 为
为![]() 或
或![]() 上的中线.
上的中线.
故当取![]() ,且
,且![]() 时,
时,![]() 最短;
最短;
当![]() 与
与![]() 重合且
重合且![]() 为
为![]() 中点,或
中点,或![]() 与
与![]() 重合且
重合且![]() 为
为![]() 中点时,
中点时,![]() 最长.
最长.

 名校课堂系列答案
名校课堂系列答案【题目】下表数据为某地区某种农产品的年产量x(单位:吨)及对应销售价格y(单位:千元/吨) .
x | 1 | 2 | 3 | 4 | 5 |
y | 70 | 65 | 55 | 38 | 22 |
(1)若y与x有较强的线性相关关系,根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程.
(2)若该农产品每吨的成本为13.1千元,假设该农产品可全部卖出,利用上问所求的回归方程,预测当年产量为多少吨时,年利润Z最大?
(参考公式:回归直线方程为![]() ,
,![]() ,
,![]() )
)
【题目】为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如右下表所示(![]() (吨)为买进蔬菜的质量,
(吨)为买进蔬菜的质量,![]() (天)为销售天数):
(天)为销售天数):
(Ⅰ) 根据右表提供的数据在网格中绘制散点图,并判断![]() 与
与![]() 是否线性相关,若线性相关,用最小二乘法求出
是否线性相关,若线性相关,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()

| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅱ)根据(Ⅰ)中的计算结果,若该蔬菜商店准备一次性买进蔬菜25吨,则预计需要销售多少天.
参考公式: ,
,![]()