题目内容
【题目】如图,已知![]() 是正三角形,EA,CD都垂直于平面ABC,且
是正三角形,EA,CD都垂直于平面ABC,且![]() ,
,![]() ,F是BE的中点,
,F是BE的中点,

求证:(1)![]() 平面ABC;
平面ABC;
(2)![]() 平面EDB.
平面EDB.
(3)求几何体![]() 的体积.
的体积.
【答案】(1)见解析(2)见解析(3)![]()
【解析】
(1)如图:证明![]() 得到答案.
得到答案.
(2)证明![]() 得到答案.
得到答案.
(3)几何体![]() 转化为
转化为![]() ,利用体积公式得到答案.
,利用体积公式得到答案.
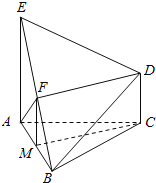
(1)∵F分别是BE的中点,取BA的中点M,
∴FM∥EA,FM![]() EA=1
EA=1
∵EA、CD都垂直于平面ABC,∴CD∥EA,
∴CD∥FM,又CD=FM
∴四边形FMCD是平行四边形,∴FD∥MC,
FD平面ABC,MC平面ABC
∴FD∥平面ABC.
(2)因M是AB的中点,△ABC是正三角形,所以CM⊥AB
又 EA垂直于平面ABC∴CM⊥AE,
又 AE∩AB=A,所以CM⊥面EAB,∵AF面EAB
∴CM⊥AF,又CM∥FD,从而FD⊥AF,
因F是BE的中点,EA=AB所以AF⊥EB.
EB,FD是平面EDB内两条相交直线,所以AF⊥平面EDB.
(3)几何体![]() 的体积等于
的体积等于![]()
![]() 为
为![]() 中点,连接
中点,连接![]()
![]() 平面
平面![]()
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目