题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() .
.
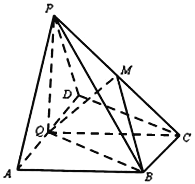
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 为棱
为棱![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)若二面角![]() 大小为
大小为![]() ,求
,求![]() 的长.
的长.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意先证明![]() ,由面面垂直的性质定理得
,由面面垂直的性质定理得![]() 平面
平面![]() ,再运用面面垂直的判定定理证明
,再运用面面垂直的判定定理证明
(2)以![]() 为原点建立空间直角坐标系,求出直线
为原点建立空间直角坐标系,求出直线![]() 与
与![]() 的向量表示,然后运用空间向量知识求出异面直线所成角的余弦值
的向量表示,然后运用空间向量知识求出异面直线所成角的余弦值
(3)结合(2)中的空间直角坐标系,运用向量知识结合二面角为![]() 求出结果
求出结果
(1)证明:![]() 为
为![]() 的中点,
的中点,
∴四边形![]() 为平行四边形,
为平行四边形,
![]()
![]() 即
即![]()
又![]() 平面
平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]()
∵![]() 平面
平面![]() , ∴平面
, ∴平面![]() 平面
平面![]()
(2)解:![]() 为
为![]() 的中点,
的中点,
![]()
∵平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
如图,以![]() 为原点建立空间直角坐标系,
为原点建立空间直角坐标系,
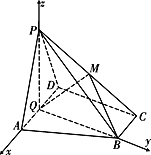
则![]() ,
,
![]() 是
是![]() 的中点,
的中点,![]()
![]()
设异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
,
则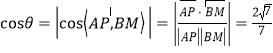
∴异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(3)解:由(2)知平面![]() 的法向量为
的法向量为![]()
由![]()
得![]()
又![]() ,
,
设平面![]() 法向量为
法向量为![]() ,
,
由![]() 可取
可取![]()
∵二面角![]() 为60°,
为60°,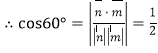 ,
,
![]()

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案【题目】为了加强中学生实践、创新和团队建设能力的培养,促进教育教学改革,市教育局举办了全市中学生创新知识竞赛,某中学举行了选拔赛,共有150名学生参加,为了了解成绩情况,从中抽取50名学生的成绩(得分均为整数,满分为100分)进行统计,请你根据尚未完成的频率分布表,解答下列问题:
(1)完成频率分布表(直接写出结果);
(2)若成绩在90.5分以上的学生获一等奖,试估计全校获一等奖的人数,现在从全校所有获一等奖的同学中随机抽取2名同学代表学校参加竞赛,某班共有2名同学荣获一等奖,求该班同学恰有1人参加竞赛的概率.
分组 | 频数 | 频率 | |
第1组 | [60.5,70.5) | 0.26 | |
第2组 | [70.5,80.5) | 17 | |
第3组 | [80.5,90.5) | 18 | 0.36 |
第4组 | [90.5,100.5] | ||
合计 | 50 | 1 |


