题目内容
【题目】设二次函数f(x)=ax2+bx+c(a≠0)在区间[﹣2,2]上的最大值、最小值分别是M,m,集合A={x|f(x)=x}.
(1)若A={1,2},且f(0)=2,求M和m的值;
(2)若A={1},且a≥1,记g(a)=M+m,求g(a)的最小值.
【答案】
(1)解:由f(0)=2可知c=2,
又A={1,2},故1,2是方程ax2+(b﹣1)x+c=0的两实根.
∴ 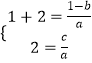 ,解得a=1,b=﹣2
,解得a=1,b=﹣2
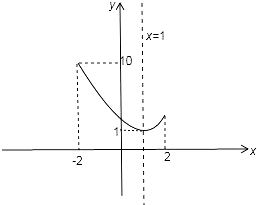
∴f(x)=x2﹣2x+2=(x﹣1)2+1,
因为x∈[﹣2,2],根据函数图象可知,当x=1时,
f(x)min=f(1)=1,即m=1;
当x=﹣2时,f(x)max=f(﹣2)=10,即M=10
(2)解:由题意知,方程ax2+(b﹣1)x+c=0有两相等实根x1=x2=1,
根据韦达定理得到: 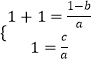 ,即
,即 ![]() ,
,
∴f(x)=ax2+bx+c=ax2+(1﹣2a)x+a,x∈[﹣2,2]其对称轴方程为x= ![]() =1﹣
=1﹣ ![]()
又a≥1,故1﹣ ![]()
∴M=f(﹣2)=9a﹣2
m= ![]()
则g(a)=M+m=9a﹣ ![]() ﹣1
﹣1
又g(a)在区间[1,+∞)上为单调递增的,∴当a=1时,g(a)min= ![]()
【解析】(1)由f(0)=2得到c的值,集合A的方程可变为f(x)﹣x=0,因为A={1,2},得到1,2是方程的解,根据韦达定理即可求出a和b,把a、b、c代入得到f(x)的解析式,在[﹣2,2]上根据函数的图象可知m和M的值.(2)由集合A={1},得到方程f(x)﹣x=0有两个相等的解都为1,根据韦达定理求出a,b,c的关系式,根据a大于等于1,利用二次函数求最值的方法求出在[﹣2,2]上的m和M,代入g(a)=m+M中得到新的解析式g(a)=9a﹣ ![]() ﹣1,根据g(a)的在[1,+∞)上单调增,求出g(a)的最小值为g(1),求出值即可.
﹣1,根据g(a)的在[1,+∞)上单调增,求出g(a)的最小值为g(1),求出值即可.
【考点精析】关于本题考查的二次函数的图象和二次函数的性质,需要了解二次函数![]() 的图象是一条抛物线,对称轴方程为
的图象是一条抛物线,对称轴方程为![]() 顶点坐标是
顶点坐标是![]() ;当
;当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能得出正确答案.
上递减才能得出正确答案.

 阅读快车系列答案
阅读快车系列答案