��Ŀ����
����Ŀ����ͼ���ں�����![]() һ��
һ��![]() ����һ��������С����ij���ι�˾Ϊ�����οͣ���
����һ��������С����ij���ι�˾Ϊ�����οͣ���![]() ��������
��������![]() ���������㣬����
���������㣬����![]() �����������ľ���Ϊ
�����������ľ���Ϊ![]() .��˾�ⰴ����˼·�������Ƚ�
.��˾�ⰴ����˼·�������Ƚ�![]() �����οͷֱ�˳����е�
�����οͷֱ�˳����е�![]() ֮�����ת��
֮�����ת��![]() ��(��
��(��![]() ����
����![]() ����)��Ȼ���ͬһ��������ǰ��
����)��Ȼ���ͬһ��������ǰ��![]() ������ͳ�ƣ�ÿ���ο�
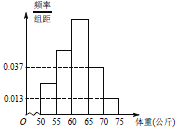
������ͳ�ƣ�ÿ���ο�![]() ���跢��2����
���跢��2���� ![]() ���跢��4����ÿ������ÿǧ�ķ�
���跢��4����ÿ������ÿǧ�ķ�![]() Ԫ������ÿǧ�ķ�
Ԫ������ÿǧ�ķ�![]() Ԫ��������
Ԫ��������![]() ��������������
��������������![]() ��ÿ���οʹӸ��Ա����㵽
��ÿ���οʹӸ��Ա����㵽![]() ����������ɱ�Ϊ
����������ɱ�Ϊ![]() Ԫ��
Ԫ��
(1) �![]() ����
����![]() �ĺ�������ʽ����ָ��
�ĺ�������ʽ����ָ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
(2) �ʣ���ת��![]() ����
����![]() ����Զʱ��
����Զʱ�� ![]() ��С��
����
���𰸡�(1) ![]() ����2��
����2��![]() .
.
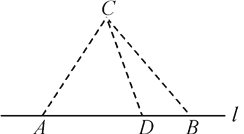
�������������������1����![]() �У������صĽǣ��������Ҷ��������
�У������صĽǣ��������Ҷ��������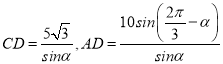 ����ʾ����������ɱ�Ϊ
����ʾ����������ɱ�Ϊ![]() Ԫ����
Ԫ����![]() �ĺ�������ʽ����2�����ú�������ʽ����������ĵ�����ͨ�������ķ��ţ��жϵ�������⺯������ֵ.
�ĺ�������ʽ����2�����ú�������ʽ����������ĵ�����ͨ�������ķ��ţ��жϵ�������⺯������ֵ.
���������(1) ����֪����ACD�У���CAD��![]() ����CDA������AC��10����ACD��
����CDA������AC��10����ACD��![]() ����.
����.
�����Ҷ���֪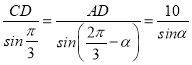 ��
��
��CD��![]() �� AD��
�� AD��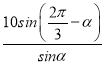 ��
��
����S��4aAD��8aBD��12aCD�� (12CD��4AD��80)a
��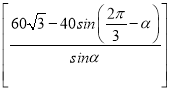 a��80a ��
a��80a ��![]() a��60a
a��60a![]()
(2) S����20 ![]() ��
��
��S����0��cos ����![]()
��cos ��>![]() ʱ��S��<0�� ��cos ��
ʱ��S��<0�� ��cos ��![]() <ʱ��S��>0��
<ʱ��S��>0��
���Ե�cos ����![]() ʱ��Sȡ����Сֵ��
ʱ��Sȡ����Сֵ��
��ʱsin ����![]() ��AD��
��AD��![]() ��5��
��5��![]() ��
��
������ת��C��A��![]() kmʱ������ɱ�S��С��
kmʱ������ɱ�S��С��

 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�