题目内容
在直角坐标系xOy中,椭圆C1: 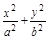 ="1" (a>b>0)的左、右焦点分别为F1、F2, F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=
="1" (a>b>0)的左、右焦点分别为F1、F2, F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=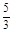 .
.
(1)求C1的方程;
(2)直线l∥OM,与C1交于A、B两点,若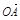 ·
·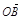 =0,求直线l的方程.
=0,求直线l的方程.
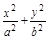 ="1" (a>b>0)的左、右焦点分别为F1、F2, F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=
="1" (a>b>0)的左、右焦点分别为F1、F2, F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=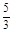 .
.(1)求C1的方程;
(2)直线l∥OM,与C1交于A、B两点,若
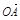 ·
·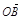 =0,求直线l的方程.
=0,求直线l的方程.(1)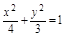 .(2)直线l的方程为y=
.(2)直线l的方程为y=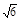 x-2
x-2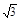 ,或y=
,或y=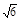 x+2
x+2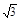 .
.
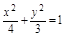 .(2)直线l的方程为y=
.(2)直线l的方程为y=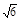 x-2
x-2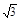 ,或y=
,或y=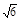 x+2
x+2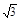 .
.试题分析:(1)由C2:y2=4x,知F2(1,0),设M(x1,y1),M在C2上,因为|MF2|=
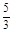 ,所以x1+1=
,所以x1+1=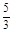 ,得x1=
,得x1=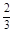 ,y1=
,y1=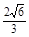 .所以M
.所以M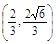 .M在C1上,且椭圆C1的半焦距c=1,于是
.M在C1上,且椭圆C1的半焦距c=1,于是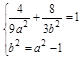 消去b2并整理得9a4-37a2+4=0.
消去b2并整理得9a4-37a2+4=0.解得a=2(a=
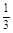 不合题意,舍去). b2=4-1=3.故椭圆C1的方程为
不合题意,舍去). b2=4-1=3.故椭圆C1的方程为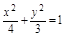 .
.(2)因为l∥OM,所以l与OM的斜率相同.故l的斜率k=
 =
=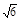 .设l的方程为y=
.设l的方程为y=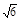 (x-m).
(x-m).由
 消去y并整理得9x2-16mx+8m2-4=0.设A(x1,y1),B(x2,y2),则x1+x2=
消去y并整理得9x2-16mx+8m2-4=0.设A(x1,y1),B(x2,y2),则x1+x2=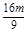 ,x1x2=
,x1x2=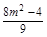 .
.因为
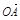 ⊥
⊥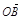 ,所以x1x2+y1y2=0.所以x1x2+y1y2=x1x2+6(x1-m)(x2-m)=7x1x2-6m(x1+x2)+6m2
,所以x1x2+y1y2=0.所以x1x2+y1y2=x1x2+6(x1-m)(x2-m)=7x1x2-6m(x1+x2)+6m2=7·
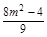 -6m·
-6m·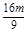 +6m2=
+6m2=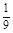 (14m2-28)=0.所以m=±
(14m2-28)=0.所以m=± .此时Δ=(16m)2-4×9(8m2-4)>0.
.此时Δ=(16m)2-4×9(8m2-4)>0.故所求直线l的方程为y=
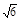 x-2
x-2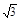 ,或y=
,或y=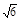 x+2
x+2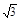 .
.点评:难题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题求椭圆标准方程时,主要运用了椭圆的几何性质,通过布列方程,达到解题目的。本题(2)在利用韦达定理的基础上,借助于向量垂直,向量的数量积为0,得到了m的方程。

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
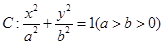 的离心率为
的离心率为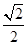 ,
,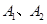 是椭圆的左右顶点,
是椭圆的左右顶点,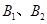 是椭圆的上下顶点,四边形
是椭圆的上下顶点,四边形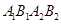 的面积为
的面积为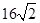 .
.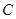 的方程;
的方程;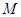 过
过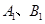 两点.当圆心
两点.当圆心 的距离最小时,求圆
的距离最小时,求圆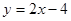 与抛物线
与抛物线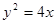 交于
交于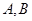 两点.
两点.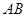 的长;(2)若抛物线
的长;(2)若抛物线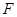 ,求
,求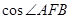 的值.
的值.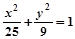 (y≠0)
(y≠0)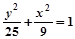 (y≠0)
(y≠0)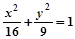 (y≠0)
(y≠0)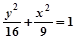 (y≠0)
(y≠0)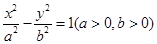 与椭圆
与椭圆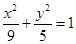 有相同的焦点
有相同的焦点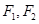 ,且该双曲线
,且该双曲线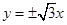 .
.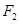 作斜率不为零的直线与此双曲线的左,右两支分别交于点
作斜率不为零的直线与此双曲线的左,右两支分别交于点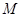 、
、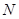 ,
,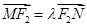 ,当
,当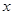 轴上的点
轴上的点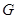 满足
满足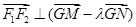 时,求点
时,求点 O
O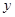 中,直线
中,直线 与抛物线
与抛物线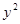 =2
=2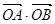 =3”是真命题;
=3”是真命题;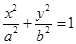 (a>b>0)的两焦点为F1、F2,若椭圆上存在一点Q,使∠F1QF2=120º,椭圆离心率e的取值范围为( )
(a>b>0)的两焦点为F1、F2,若椭圆上存在一点Q,使∠F1QF2=120º,椭圆离心率e的取值范围为( )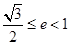
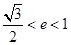
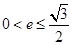

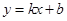 与曲线
与曲线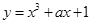 相切于点
相切于点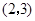 ,则
,则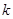 的值为 ( )
的值为 ( )