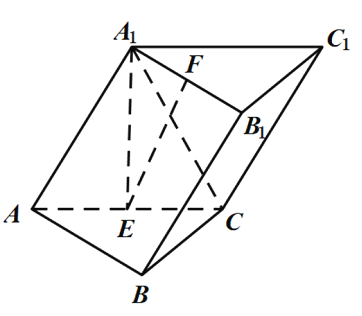
题目内容
【题目】已知函数![]()
(1)讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,当函数
,当函数![]() 与
与![]() 的图象有三个不同的交点时,求实数
的图象有三个不同的交点时,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2) ![]()
【解析】
(1)对函数![]() 求导,根据
求导,根据![]() 的不同取值,结合不等式,可以判断出函数的单调性;
的不同取值,结合不等式,可以判断出函数的单调性;
(2)由题意可知:![]() ,得
,得![]() .得
.得![]() ,
,
设![]() ,则
,则![]() 有三个不同的根等价于函数
有三个不同的根等价于函数![]() 存在三个不同的零点.对函数
存在三个不同的零点.对函数![]() 进行求导,然后判断出其单调性,结合零点存在原理,最后求出实数
进行求导,然后判断出其单调性,结合零点存在原理,最后求出实数![]() 的取值范围.
的取值范围.
(1)![]() 的定义域是
的定义域是![]() ,
,
![]() ,
,
当![]() 时.
时.![]() 两数
两数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,令
时,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() .
.
故函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单洞递破.
上单洞递破.
(2)由![]() ,得
,得![]() .得
.得![]() ,
,
设![]() ,则
,则![]() 有三个不同的根等价于函数
有三个不同的根等价于函数![]() 存在三个不同的零点.
存在三个不同的零点.
![]() ,
,
当![]() 即
即![]() 时,
时,![]() ,
,![]() 单调递减,不可能有三个不同的零点,
单调递减,不可能有三个不同的零点,
当![]() 即
即![]() ,
,![]() 有两个零点
有两个零点![]() ,
,
![]() ,
,
又![]() 开口向下,
开口向下,
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递诫:
上单调递诫:
当![]() 时.
时.![]() 函数
函数![]() 在
在![]() 上单调递增:
上单调递增:
当![]() 时.
时.![]() ,函数
,函数![]() 在
在![]() 上单调递减.
上单调递减.
因为![]() ,又
,又![]() ,有
,有![]() ,
,
所以![]()
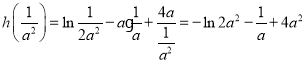 ,
,
令![]() .则
.则![]() .
.
令![]() .则
.则![]() 单调递增.
单调递增.
由![]() ,求得
,求得![]() ,
,
当![]() 时,
时,![]() 单调递减,
单调递减,![]() .,
.,
显然在![]() 上单调递增,
上单调递增,
故![]() .
.
由零点存在性定理知![]() 在区间
在区间![]() 上有一个根.设为
上有一个根.设为![]() ,
,
又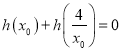 .得
.得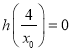 .所以
.所以![]() .所以
.所以![]() 是
是![]() 的另一个零点,
的另一个零点,
故当![]() 时,
时,![]() 存在三个不同的零点
存在三个不同的零点![]() .
.
故实数![]() 的取值范围是
的取值范围是![]() .
.

【题目】人们常说的“幸福感指数”就是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间![]() 内的一个数来表示,该数越接近
内的一个数来表示,该数越接近![]() 表示满意度越高.为了解某地区居民的幸福感情况,随机对该地区的男、女居民各
表示满意度越高.为了解某地区居民的幸福感情况,随机对该地区的男、女居民各![]() 人进行了调查,调查数据如表所示:
人进行了调查,调查数据如表所示:
幸福感指数 |
|
|
|
|
|
男居民人数 |
|
|
|
|
|
女居民人数 |
|
|
|
|
|
(1)估算该地区居民幸福感指数的平均值;
(2)若居民幸福感指数不小于![]() ,则认为其幸福.为了进一步了解居民的幸福满意度,调查组又在该地区随机抽取
,则认为其幸福.为了进一步了解居民的幸福满意度,调查组又在该地区随机抽取![]() 对夫妻进行调查,用
对夫妻进行调查,用![]() 表示他们之中幸福夫妻(夫妻二人都感到幸福)的对数,求
表示他们之中幸福夫妻(夫妻二人都感到幸福)的对数,求![]() 的期望(以样本的频率作为总体的概率).
的期望(以样本的频率作为总体的概率).
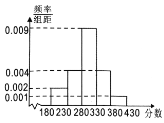
【题目】某校高三实验班的60名学生期中考试的语文、数学成绩都在![]() 内,其中语文成绩分组区间是:
内,其中语文成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .其成绩的频率分布直方图如图所示,这60名学生语文成绩某些分数段的人数
.其成绩的频率分布直方图如图所示,这60名学生语文成绩某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示:
之比如下表所示:
分组区间 |
|
|
|
|
|
|
|
|
|
| |
语文人数 | 24 | 3 | |||
数学人数 | 12 | 4 |
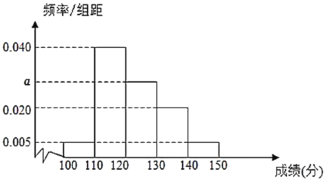
(1)求图中![]() 的值及数学成绩在
的值及数学成绩在![]() 的人数;
的人数;
(2)语文成绩在![]() 的3名学生均是女生,数学成绩在
的3名学生均是女生,数学成绩在![]() 的4名学生均是男生,现从这7名学生中随机选取4名学生,事件
的4名学生均是男生,现从这7名学生中随机选取4名学生,事件![]() 为:“其中男生人数不少于女生人数”,求事件
为:“其中男生人数不少于女生人数”,求事件![]() 发生的概率;
发生的概率;
(3)若从数学成绩在![]() 的学生中随机选取2名学生,且这2名学生中数学成绩在
的学生中随机选取2名学生,且这2名学生中数学成绩在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.