题目内容
【题目】如图,在正方体![]() 中,
中,![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 是底面
是底面![]() 内一点,且
内一点,且![]() 平面
平面![]() ,则
,则![]() 的最大值是( )
的最大值是( )

A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
【答案】C
【解析】分析:连结AC、BD,交于点O,连结A1C1,交EF于M,连结OM,则AO![]() PM,从而A1P=C1M,由此能求出tan∠APA1的最大值.
PM,从而A1P=C1M,由此能求出tan∠APA1的最大值.
详解:连结AC、BD,交于点O,连结A1C1,交EF于M,连结OM,
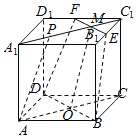
设正方形ABCD﹣A1B1C1D1中棱长为1,
∵在正方形ABCD﹣A1B1C1D1中,E,F分别为B1C1,C1D1的中点,
点P是底面A1B1C1D1内一点,且AP∥平面EFDB,
∴AO![]() PM,∴A1P=C1M=
PM,∴A1P=C1M=![]() ,
,
∴tan∠APA1=![]() =
=![]() =2
=2![]() .
.
∴tan∠APA1的最大值是2![]() .
.
故选:D.

练习册系列答案
相关题目