题目内容
14．已知函数f（x）的周期为1.5，且f（1）=20，则f（13）的值是20．分析 根据已知中函数的周期性，可得f（13）=f（1.5×8+1）=f（1），进而得到答案．
解答 解：∵函数f（x）的周期为1.5，且f（1）=20，
∴f（13）=f（1.5×8+1）=f（1）=20．
故答案：20
点评 本题考查的知识点是函数的周期性，函数求值，难度不大，属于基础题．
练习册系列答案
相关题目
2．设P为△ABC内一点，且$\overrightarrow{AP}=\frac{3}{7}\overrightarrow{AB}+\frac{2}{7}\overrightarrow{AC}$，则△ABP与△ACP的面积之比为（ ）
| A． | 3：2 | B． | 2：3 | C． | 3：7 | D． | 7：2 |
9．若向量$\overrightarrow a$=（1，2），$\overrightarrow{b}$=（1，-1），则2$\overrightarrow a$+$\overrightarrow{b}$与$\overrightarrow a$-$\overrightarrow{b}$的夹角等于（ ）
| A． | -$\frac{π}{4}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{4}$ | D． | $\frac{3π}{4}$ |
19．不等式2kx2+kx-$\frac{3}{8}$＜0对任何实数x恒成立，则k的取值范围是（ ）
| A． | （-3，0] | B． | （-3，0） | C． | [-3，0] | D． | [-3，0） |
6．在△ABC中，内角A，B，C的对边分别为a、b、c，且a、b、c成等比数列，a+c=3，tanB=$\frac{{\sqrt{7}}}{3}$，则△ABC的面积为（ ）
| A． | $\frac{{\sqrt{7}}}{2}$ | B． | $\frac{7}{2}$ | C． | $\frac{5}{2}$ | D． | $\frac{{\sqrt{7}}}{4}$ |
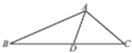如图，在△ABC中，AB=3，AC=2，BC=4，点D在边BC上，∠BAD=30°，则sin∠CAD的值为$\frac{3\sqrt{5}+1}{8}$．