题目内容
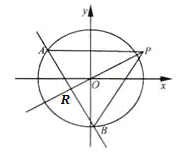
【题目】如图所示,在棱长为1的正方体![]() 中,点
中,点![]() 在
在![]() 上移动,点
上移动,点![]() 在
在![]() 上移动,
上移动,![]() ,连接
,连接![]() .
.

(1)证明:对任意![]() ,总有
,总有![]() 平面
平面![]() ;
;
(2)当![]() 为何值时,
为何值时,![]() 的长度最小?
的长度最小?
【答案】(1)证明见解析(2)![]()
【解析】
(1)作![]() ,交
,交![]() 于点
于点![]() ,作
,作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,根据平行线成比例定理,结合已知,可以证明出四边形
,根据平行线成比例定理,结合已知,可以证明出四边形![]() 为平行四边形,利用平行四边形的性质,线面平行的判定定理证明即可;
为平行四边形,利用平行四边形的性质,线面平行的判定定理证明即可;
(2)根据平行线成比例定理,通过计算可以求出![]() 的值,利用勾股定理求出
的值,利用勾股定理求出![]() 的表达式,运用配方法求出
的表达式,运用配方法求出![]() 的长度最小值.
的长度最小值.
(1)证明:如图,作![]() ,交
,交![]() 于点
于点![]() ,作
,作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
因为![]() 是正方形,所以有
是正方形,所以有![]() ,因此有
,因此有![]() ,因为
,因为![]() ,所以
,所以![]() ,同理可证明
,同理可证明![]() ,因此
,因此![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,![]() .又
.又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
(2)由(1)知四边形![]() 为平行四边形,
为平行四边形,![]() .
.
![]() ,
,
![]() ,
,
即![]() ,
,
![]()
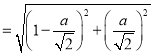
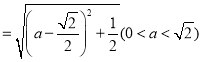
故当![]() 时,
时,![]() 的长度有最小值,最小值为
的长度有最小值,最小值为![]() .
.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】随着手机的普及,大学生迷恋手机的现象非常严重.为了调查双休日大学生使用手机的时间,某机构采用不记名方式随机调查了使用手机时间不超过10小时的50名大学生,将50人使用手机的时间分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别加以统计,得到下表,根据数据完成下列问题:
分别加以统计,得到下表,根据数据完成下列问题:
使用时间/时 |
|
|
|
|
|
大学生/人 | 5 | 10 | 15 | 12 | 8 |

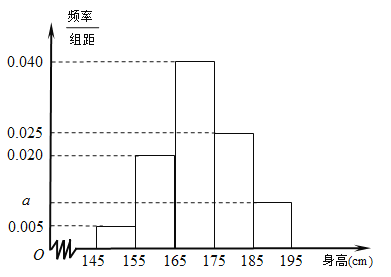
(1)完成频率分布直方图,并根据频率分布直方图估计大学生使用手机时间的中位数(保留小数点后两位);
(2)用分层抽样的方法从使用手机时间在区间![]() ,
,![]() ,
,![]() 的大学生中抽取6人,再从这6人中随机抽取2人,求这2人取自不同使用时间区间的概率.
的大学生中抽取6人,再从这6人中随机抽取2人,求这2人取自不同使用时间区间的概率.