题目内容
12.设椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1上一点P,点P在第一象限,且OP与x轴正方向所成角∠POX=$\frac{π}{3}$,求点P的坐标.分析 设直线OP的方程为y=$\sqrt{3}$x,代入椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1,利用点P在第一象限,即可求点P的坐标.
解答 解:设直线OP的方程为y=$\sqrt{3}$x,
代入椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1,可得椭圆$\frac{{x}^{2}}{16}$+$\frac{3{x}^{2}}{12}$=1,
∵点P在第一象限,
∴x=$\frac{4\sqrt{15}}{15}$,y=$\frac{4\sqrt{5}}{5}$.
∴P($\frac{4\sqrt{15}}{15}$,$\frac{4\sqrt{5}}{5}$).
点评 本题考查直线与椭圆的位置关系,考查学生的计算能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
3.已知函数f(x)=$\left\{\begin{array}{l}{|{2}^{x}-1|(x<1)}\\{-(x-2)^{2}+1(x≥1)}\end{array}\right.$,则关于x的方程f(x+$\frac{1}{x}$-1)=a的实根个数最多为( )
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
20.已知函数f(x)=ln(1-$\frac{a}{x+1}$)(a∈R),命题p:?a∈R,f(x)是奇函数,命题q:?a∈R,f(x)在定义域内是增函数,那么下列命题是真命题的是( )
| A. | ¬p | B. | p∧q | C. | (¬p)∧q | D. | p∧(¬q) |
17.一个几何体的三视图如图所示,则该几何体的体积为( )
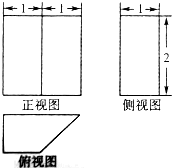

| A. | $\frac{2}{3}$ | B. | 1 | C. | 3 | D. | 6 |
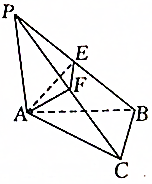 如图所示,已知在△ABC中,∠C=90°,PA⊥平面ABC,AE⊥PB交PB于E,AF⊥PC于F,AP=AB=2,∠AEF=θ,当θ变化时,求三棱锥P-AEF的体积的最大值.
如图所示,已知在△ABC中,∠C=90°,PA⊥平面ABC,AE⊥PB交PB于E,AF⊥PC于F,AP=AB=2,∠AEF=θ,当θ变化时,求三棱锥P-AEF的体积的最大值.