题目内容
7.某中学为了解学校办公楼每天的用电量x(度)与当天最高气温x(℃)之间的关系,随机统计了近期某4天的有关数据如下表示:| 最高气温x(℃) | 10 | 4 | -2 | -8 |
| 用电量y(度) | 20 | 44 | 56 | 80 |
| A. | 32度 | B. | 34度 | C. | 36度 | D. | 38度 |
分析 首先求出x,y的平均数,根据所给的线性回归方程知道b的值,根据样本中心点满足线性回归方程,把样本中心点代入,得到关于a的一元一次方程,解方程求出a值,再将x=6代入可得答案.
解答 解:由表格知样本中心点为$(\overline{x},\overline{y})=(\frac{4}{4},\frac{200}{4})=(1,50)$,
则回归方程是$\widehat{y}$=-3.2x+a,
将(1,50)点代入得:a=53.2,
则回归方程是$\widehat{y}$=-3.2x+53.2,
则当x=6时,y的预测值为$\hat{y}=-3.2×6+53.2=34$,
故选:B.
点评 本题考查回归分析,考查样本中心点满足回归直线的方程,考查求一组数据的平均数,是一个运算量比较小的题目.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
15.已知sinx+cosx=$\sqrt{1+sin2x}$,则x的取值范围是( )
| A. | [-$\frac{π}{4}$+kπ,$\frac{π}{4}$+kπ](k∈Z) | B. | [$\frac{π}{4}$+kπ,$\frac{3π}{4}$+kπ](k∈Z) | ||
| C. | [-$\frac{π}{4}$+2kπ,$\frac{3π}{4}$+2kπ](k∈Z) | D. | [$\frac{π}{4}$+2kπ,$\frac{5π}{4}$+2kπ](k∈Z) |
16.运行如图的程序框图,则输出s的结果是( )
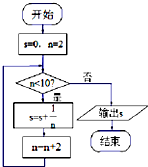

| A. | $\frac{25}{24}$ | B. | $\frac{1}{6}$ | C. | $\frac{3}{4}$ | D. | $\frac{11}{12}$ |
17.一个几何体的三视图如图所示,则该几何体的体积为( )
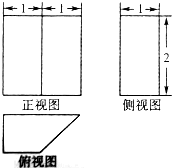

| A. | $\frac{2}{3}$ | B. | 1 | C. | 3 | D. | 6 |