题目内容
【题目】设x>0,y>0,已知( ![]() ﹣x+1)(
﹣x+1)( ![]() ﹣y+1)=2,则xy﹣2=
﹣y+1)=2,则xy﹣2=
【答案】﹣1
【解析】解:设x=tanα>0,y=tanβ>0,
则( ![]() ﹣x+1)(
﹣x+1)( ![]() ﹣y+1)=2
﹣y+1)=2
即为( ![]() ﹣tanα+1)(
﹣tanα+1)( ![]() ﹣tanβ+1)=2,
﹣tanβ+1)=2,
即有(secα﹣tanα+1)(secβ﹣tanβ+1)=2,
即 ![]()
![]() =2,
=2,
由  =
= 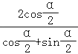 =
= 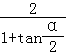 ,
,
可得 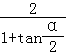
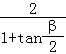 =2,
=2,
即有(1+tan ![]() )(1+tan
)(1+tan ![]() )=2,
)=2,
即tan ![]() +tan
+tan ![]() =1﹣tan
=1﹣tan ![]() tan
tan ![]() ,
,
可得tan ![]() =
= 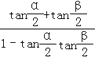 =1,
=1,
由α,β为锐角,可得 ![]() =45°,
=45°,
则α+β=90°,
即有xy﹣2=tanαtanβ﹣2=tanαtan(90°﹣α)﹣2
=tanαcotα﹣2=1﹣2=﹣1.
所以答案是:﹣1.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目