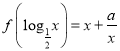题目内容
【题目】设集合A是实数集R的子集,如果x0∈R满足:对任意a>0,都存在x∈A,使得0<|x﹣x0|<a,则称x0为集合A的聚点,给出下列集合(其中e为自然对数的底):①{1+ ![]() |x>0};②{2x|x∈N};③{x2+x+2|x∈R};④{lnx|x>0且x≠e},其中,以1为聚点的集合有( )
|x>0};②{2x|x∈N};③{x2+x+2|x∈R};④{lnx|x>0且x≠e},其中,以1为聚点的集合有( )
A.①②
B.②③
C.③④
D.①④
【答案】D
【解析】解:①{1+ ![]() |x>0}中的元素构成以1为极限的数列,故对任意a>0,都存在x∈A,使得0<|x﹣1|<a成立,符合题意;
|x>0}中的元素构成以1为极限的数列,故对任意a>0,都存在x∈A,使得0<|x﹣1|<a成立,符合题意;
②{2x|x∈N},y=2x是单调增函数,对任意a>0,不存在x∈A,使得0<|x﹣1|<a,不符合题意;
③{x2+x+2|x∈R},∵x2+x+2≥ ![]() ,对任意a>0,不存在x∈A,使得0<|x﹣1|<a,不符合题意;
,对任意a>0,不存在x∈A,使得0<|x﹣1|<a,不符合题意;
④{lnx|x>0且x≠e},lnx≠1,满足:对任意a>0,都存在x∈A,使得0<|x﹣1|<a,故此集合以1为聚点符合题意,
故选:D.
【考点精析】通过灵活运用子集与真子集,掌握任何一个集合是它本身的子集;n个元素的子集有2n个,n个元素的真子集有2n -1个,n个元素的非空真子集有2n-2个即可以解答此题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目