题目内容
【题目】二次函数f（x）的图象与x轴交于（﹣2，0），（4，0）两点，且顶点为（1，﹣ 
）．
（1）求f（x）的函数解析式；
（2）指出图象的开口方向、对称轴和顶点坐标；
（3）分析函数的单调性，求函数的最大值或最小值．
【答案】
（1）解：二次函数f（x）的图象与x轴交于（﹣2，0），（4，0）两点，
故设函数的解析式为：f（x）=a（x+2）（x﹣4），
将（1，﹣ 
）代入函数的解析式得：a= 
，
故f（x）= （x﹣1）2﹣
（2）解：由（1）得：
图象开口向上，对称轴方程x=1，顶点坐标（1，﹣ ）
（3）解：由（1）f（x）的单调减区间为（﹣∞，1]，单调增区间为[1，+∞），
无最大值，最小值为﹣
【解析】（1）设出二次函数的解析式，代入顶点，求出函数的解析式即可；（2）根据函数的解析式判断出图象的开口方向、对称轴和顶点坐标即可；（3）求出函数的对称轴，得到函数的单调区间，从而求出函数的最值即可．
【考点精析】本题主要考查了函数单调性的判断方法和二次函数的性质的相关知识点，需要掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较；当
时，抛物线开口向上，函数在
上递减，在
上递增；当
时，抛物线开口向下，函数在上递增，在上递减才能正确解答此题．
【题目】某学校高三年级有学生500人，其中男生300人，女生200人，为了研究学生的数学成绩是否与性别有关，现采用分层抽样的方法，从中抽取了100名学生，先统计了他们期中考试的数学分数，然后按性别分为男、女两组，再将两组学生的分数分成5组：[100，110)，[110，120)，[120，130)，[130，140)，[140，150]分别加以统计，得到如图所示的频率分布直方图．
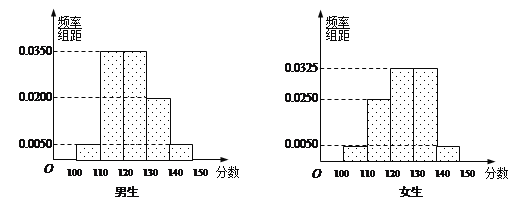
（1）从样本中分数小于110分的学生中随机抽取2人，求两人恰好为一男一女的概率；
（2）若规定分数不小于130分的学生为“数学尖子生”，请你根据已知条件完成2×2列联表，并判断是否有90%的把握认为“数学尖子生与性别有关”？
附：
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
，
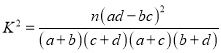