题目内容
【题目】在中学生综合素质评价某个维度的测评中，分优秀、合格、尚待改进三个等级进行学生互评.某校高一年级有男生500人，女生400人，为了了解性别对该维度测评结果的影响，采用分层抽样方法从高一年级抽取了45名学生的测评结果，并作出频数统计表如下：
表一：男生
表二：女生
（1）从表二的非优秀学生中随机抽取2人交谈，求所选2人中恰有1人测评等级为合格的概率；
（2）由表中统计数据填写下面的
列联表，并判断是否有90%的把握认为“测评结果优秀与性别有关”.
参考公式： 
，其中
.
参考数据：
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
【答案】（1）
.（2）见解析.
【解析】试题分析：（1）根据分层抽样的规则可得设从高一年级男生中抽出
人，则
， 
，然后求出女生人数即可得x，y值然后写出基本事件，根据古典概型求概率即可（2）对于独立性检验首先写出列联表，然后根据公式计算即可
试题解析：
（1）设从高一年级男生中抽出
人，则
， 
，则从女生中抽取20人，
所以
， 
.
表二中非优秀学生共5人，记测评等级为合格的3人为
， 
， 
，尚待改进的2人为
， 
，则从这5人中任选2人的所有可能结果为
， 
， 
， 
， 
， 
， 
， 
， 
， 
，共10种，
设事件
表示“从表二的非优秀学生中随机选取2人，恰有1人测评等级为合格”，则
的结果为
， 
， 
， 
， 
， 
，共6种，所以
，即所求概率为
.
（2）
列联表如下：
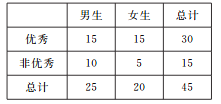
因为
， 
，
而
，所以没有90%的把握认为“测评结果优秀与性别有关”.
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
