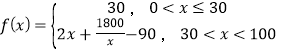题目内容
【题目】已知数列{an}的前n项和Sn= 
﹣ 
（n∈N*）．
（1）求数列{an}的通项公式；
（2）若bn=anlog3an ， 求数列{bn}的前n项和．
【答案】
（1）解：因为Sn= 
﹣ 
，
当n≥2时，Sn﹣1= 
﹣ ，
两式相减得：an=3n，
因为a1=S1=3也满足．
综上，an=3n（n∈N*）；
（2）解：bn=anlog3an=3nn，
则数列{bn}的前n项和Tn=13+29+327+…+3nn，
3Tn=19+227+381+…+3n+1n，
两式相减得：﹣2Tn=3+9+27+…+3n﹣3n+1n
= 
﹣3n+1n，
化简得：Tn= 
【解析】（1）将n换为n﹣1，两式相减，再由n=1，检验即可得到所求数列的通项公式；（2）求出bn=anlog3an=3nn，再由数列的求和方法：错位相减法，结合等比数列的求和公式，计算即可得到所求和．
【考点精析】本题主要考查了数列的前n项和的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系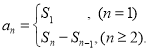
才能正确解答此题．
【题目】已知变量
之间的线性回归方程为
，且变量之间的一组相关数据如表所示，则下列说法错误的是（ ）
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量之间呈现负相关关系
B. 
的值等于5
C. 变量之间的相关系数
D. 由表格数据知，该回归直线必过点（9，4）
【题目】某学校为了制定治理学校门口上学、放学期间家长接送孩子乱停车现象的措施，对全校学生家长进行了问卷调查.根据从中随机抽取的50份调查问卷，得到了如下的列联表：
同意限定区域停车 | 不同意限定区域停车 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
则认为“是否同意限定区域停产与家长的性别有关”的把握约为__________．
附：
，其中
.
| 0.050 | 0.005 | 0.001 |
| 3.841 | 7.879 | 10.828 |
