题目内容
【题目】某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示. 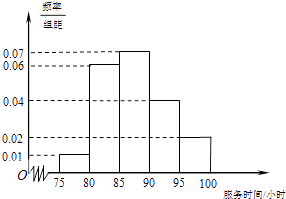
(1)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(2)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.
【答案】
(1)解:由题意可知,
参加社区服务在时间段[90,95)的学生人数为20×0.04×5=4(人),
参加社区服务在时间段[95,100]的学生人数为20×0.02×5=2(人).
所以参加社区服务时间不少于90小时的学生人数为 4+2=6(人).
(2)解:设所选学生的服务时间在同一时间段内为事件A.
由(1)可知,
参加社区服务在时间段[90,95)的学生有4人,记为a,b,c,d;
参加社区服务在时间段[95,100]的学生有2人,记为A,B.
从这6人中任意选取2人有ab,ac,ad,aA,aB,bc,bd,bA,bB,cd,cA,cB,dA,dB,AB
共15种情况.
事件A包括ab,ac,ad,bc,bd,cd,AB共7种情况.
所以所选学生的服务时间在同一时间段内的概率 ![]()
【解析】(1)利用频率分布直方图,求出频率,进而根据频数=频率×样本容量,得到答案;(2)先计算从参加社区服务时间不少于90小时的学生中任意选取2人的情况总数,再计算所选学生的参加社区服务时间在同一时间段内的情况数,代入古典概型概率计算公式,可得答案.

练习册系列答案
相关题目