题目内容
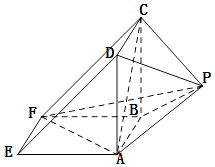
【题目】如图,已知四边形ABCD是边长为1的正方形,PA⊥平面ABCD,N是PC的中点.
(Ⅰ)若PA=1,求二面角B﹣PC﹣D的大小;
(Ⅱ)求AN与平面PCD所成角的正弦值的最大值.
【答案】解:(Ⅰ)四边形ABCD是边长为1的正方形,PA⊥平面ABCD,作BM⊥PC,连接MD,
由于RT△PBC≌RT△PDC,
则DM⊥PC,∴∠BMD就是所求二面角的平面角.
PA=AB=1,∴ ![]() ,∴
,∴ ![]() .
.
同理 ![]() ,又
,又 ![]() ,
,
在△BDM中,
由余弦定理得 ![]() ,
,
二面角B﹣PC﹣D的大小为 ![]() .
.
(Ⅱ)设AN与平面PCD所成角为α,PA=h.
作AQ⊥PD又CD⊥AQ,∴AQ⊥平面PCD,
因此在RT△AQN中, ![]() .
.
∵在RT△PAD中, ![]() ,
,
在RT△PAC中, ![]() ,
,  ,
,
∵ ![]() ,
,![]() .
.

【解析】(Ⅰ)四边性ABCD是边长为1的正方形,PA⊥平面ABCD,作BM⊥PC,连接MD,可得RT△PBC≌RT△PDC,DM⊥PC,因此∠BMD就是所求二面角的平面角.再利用余弦定理即可得出.(II)设AN与平面PCD所成角为α,PA=h.作AQ⊥PD,又CD⊥AQ,可得AQ⊥平面PCD,利用直角三角形的边角关系可得: ![]() ,再利用基本不等式的性质即可得出.
,再利用基本不等式的性质即可得出.
【考点精析】关于本题考查的空间角的异面直线所成的角,需要了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 才能得出正确答案.
才能得出正确答案.

练习册系列答案
相关题目