题目内容
【题目】如图,在正方体ABCD﹣A'B'C'D'中,点P在线段AD'上,且AP≤ ![]() AD'则异面直线CP与BA'所成角θ的取值范围是 .
AD'则异面直线CP与BA'所成角θ的取值范围是 . 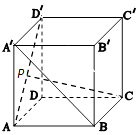
【答案】[ ![]() ,
, ![]() ]
]
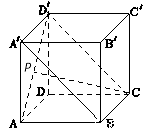
【解析】解:如图,ABCD﹣A'B'C'D'是正方体,连结CD',则异面直线CP与BA'所成的角θ等于∠D'CP,
由图可知,当P点与A点重合时,可得θ= ![]() .
.
当P点无限接近D'点时,θ趋近于0,
∵AP≤ ![]() AD',故得P在AD'中点时,θ最小,
AD',故得P在AD'中点时,θ最小,
设正方体的边长为1,则AD'= ![]() ,CD'=
,CD'= ![]() ,PC=
,PC= ![]()
AP= ![]() AD'=
AD'= ![]() ,
,
即: ![]() =
= ![]()
∴ ![]() .
.
所以异面直线CP与BA'所成角θ的取值范围是[ ![]() ,
, ![]() ].
].
所以答案是:[ ![]() ,
, ![]() ].
].
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目