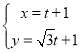Question

【题目】已知常数，数列满足，.

(1)若，，求的值；

(2)在(1)的条件下，求数列的前项和；

(3)若数列中存在三项，，(且)依次成等差数列,求的取值范围.

Answer 1

【答案】(1)；(2)，；（3）.

【解析】

（1）根据题中条件，逐项计算，即可得出结果；

（2）由（1）得到，，当时，，从而，得出，由等比数列的求和公式，即可得出结果；

（3）先由，得到数列是递增数列，分，，三种情况，利用放缩法，以及等差中项的概念，即可得出结果.

（1）因为，，

所以，

因此，，

；

（2）因为，，

所以，当时，，从而，

于是有：；

当时，；

当时，，

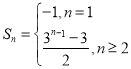所以，即，；

（3）因为，

所以，即数列是递增数列，

①当时，有，于是有，

从而，

所以，

若数列中存在三项，，(且)依次成等差数列，

则有，即，

因为，所以，

所以不成立，因此此时数列中不存在三项，，(且)依次成等差数列；

②当时，有，

此时，

于是当时，，从而，

所以，

若数列中存在三项，，(且)依次成等差数列，

则有，同①可知：，于是有，

因为，所以，

因为是整数，所以，

于是，即与矛盾，

故此时数列中不存在三项，，(且)依次成等差数列；

③当时，有，，

于是，

，

此时数列中存在三项，，(且)依次成等差数列，

综上，.