题目内容
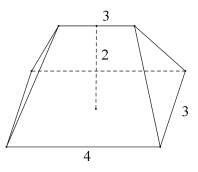
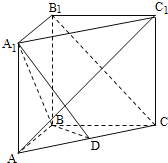
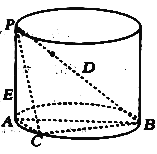
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,正方形
,正方形![]() 的边长为2,
的边长为2,![]() ,设
,设![]() 为侧棱
为侧棱![]() 的中点.
的中点.
(1)求正四棱锥![]() 的体积
的体积![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角
所成角![]() 的大小.
的大小.
【答案】(1)![]()
(2)![]()
【解析】
(1)求出点![]() 到平面
到平面![]() 的距离
的距离![]() ,正方形面积为4,再结合棱锥的体积公式求解即可;
,正方形面积为4,再结合棱锥的体积公式求解即可;
(2)建立以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴的空间直角坐标系,利用向量法求出直线
轴的空间直角坐标系,利用向量法求出直线![]() 与平面
与平面![]() 所成角
所成角![]() 的大小即可.
的大小即可.
解:(1)因为在四棱锥![]() 中,
中,![]() 平面
平面![]() ,正方形
,正方形![]() 的边长为2,
的边长为2,![]() ,又
,又![]() 为侧棱
为侧棱![]() 的中点,所以点
的中点,所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,又正方形
,又正方形![]() 的面积为
的面积为![]() ,
,
即正四棱锥![]() 的体积
的体积![]() ,
,
故正四棱锥![]() 的体积为
的体积为![]() ;
;
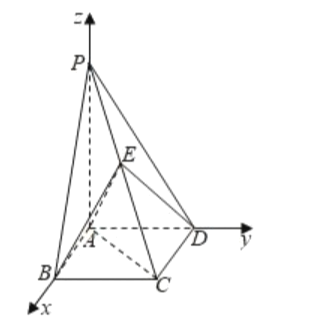
(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则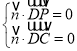 ,即
,即![]() ,令
,令![]() ,则
,则![]() ,
,
即![]() ,
,
因为直线![]() 与平面
与平面![]() 所成角
所成角![]() ,
,
所以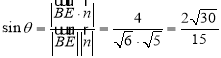 ,
,
即![]() ,
,
故直线![]() 与平面
与平面![]() 所成角
所成角![]() 的大小为
的大小为![]() .
.

练习册系列答案
相关题目
【题目】某校学生会为研究该校学生的性别与语文、数学、英语成绩这3个变量之间的关系,随机抽查了100名学生,得到某次期末考试的成绩数据如表1至表3,根据表中数据可知该校学生语文、数学、英语这三门学科中( )
表1 | 表2 | 表3 | |||||||||||||
语文 性别 | 不及格 | 及格 | 总计 | 数学 性别 | 不及格 | 及格 | 总计 | 英语 性别 | 不及格 | 及格 | 总计 | ||||
男 | 14 | 36 | 50 | 男 | 10 | 40 | 50 | 男 | 25 | 25 | 50 | ||||
女 | 16 | 34 | 50 | 女 | 20 | 30 | 50 | 女 | 5 | 45 | 50 | ||||
总计 | 30 | 70 | 100 | 总计 | 30 | 70 | 100 | 总计 | 30 | 70 | 100 | ||||
A.语文成绩与性别有关联性的可能性最大,数学成绩与性别有关联性的可能性最小
B.数学成绩与性别有关联性的可能性最大,语文成绩与性别有关联性的可能性最小
C.英语成绩与性别有关联性的可能性最大,语文成绩与性别有关联性的可能性最小
D.英语成绩与性别有关联性的可能性最大,数学成绩与性别有关联性的可能性最小