题目内容
(本小题满分13分)
已知函数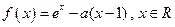 .
.
(1)若实数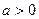 ,求函数
,求函数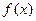 在
在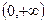 上的极值;
上的极值;
(2)记函数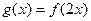 ,设函数
,设函数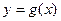 的图象C与
的图象C与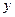 轴交于
轴交于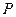 点,曲线C在
点,曲线C在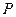 点处的切线与两坐标轴所围成的图形的面积为
点处的切线与两坐标轴所围成的图形的面积为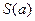 ,求当
,求当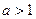 时
时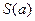 的最小值。
的最小值。
已知函数
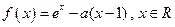 .
.(1)若实数
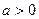 ,求函数
,求函数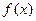 在
在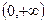 上的极值;
上的极值;(2)记函数
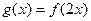 ,设函数
,设函数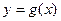 的图象C与
的图象C与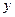 轴交于
轴交于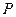 点,曲线C在
点,曲线C在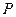 点处的切线与两坐标轴所围成的图形的面积为
点处的切线与两坐标轴所围成的图形的面积为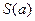 ,求当
,求当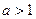 时
时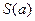 的最小值。
的最小值。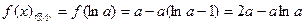 ,
,
(1)由 ,得
,得 .………………… 1分
.………………… 1分
①当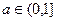 时,
时, .此时
.此时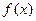 在
在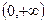 上单调递增.函数无极值。………………………………………………………………… 3分
上单调递增.函数无极值。………………………………………………………………… 3分
②当 时,
时,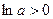 .
.
当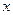 变化时
变化时 的变化情况如下表:
的变化情况如下表:
由此可得,函数有极小值且 .…… 6分
.…… 6分
(2) …………………………………… 8分
…………………………………… 8分
切线斜率为 ,切线方程
,切线方程 ,………… 10分
,………… 10分
由



当且仅当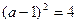 ,即
,即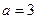 时取等号。
时取等号。
 。…………………………………………… 13分
。…………………………………………… 13分
 ,得
,得 .………………… 1分
.………………… 1分①当
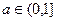 时,
时, .此时
.此时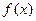 在
在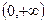 上单调递增.函数无极值。………………………………………………………………… 3分
上单调递增.函数无极值。………………………………………………………………… 3分②当
 时,
时,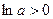 .
.当
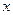 变化时
变化时 的变化情况如下表:
的变化情况如下表: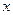 |  |  | 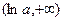 |
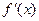 |  |  |  |
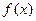 | 单减 | 极小值 | 单增 |
 .…… 6分
.…… 6分(2)
 …………………………………… 8分
…………………………………… 8分切线斜率为
 ,切线方程
,切线方程 ,………… 10分
,………… 10分由




当且仅当
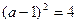 ,即
,即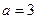 时取等号。
时取等号。 。…………………………………………… 13分
。…………………………………………… 13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
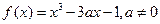 .
.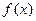 的单调区间;
的单调区间; 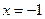 处取得极值,直线
处取得极值,直线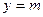 与
与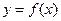 的图象有三个不同的交点,求
的图象有三个不同的交点,求 的取值范围。
的取值范围。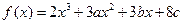 在
在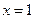 及
及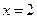 时取得极值.
时取得极值.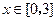 ,都有
,都有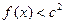 成立,求c的取值范围.
成立,求c的取值范围. 已知函数
已知函数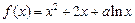 .
.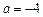 ,求函数
,求函数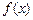 的极值;
的极值;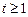 时,不等式
时,不等式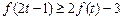 恒成立,求实数
恒成立,求实数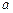 的取值范围.
的取值范围.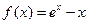 ,其中
,其中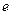 为自然对数的底数.
为自然对数的底数.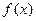 的最小值;
的最小值;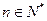 ,且
,且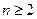 ,证明:
,证明: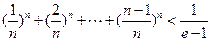 .
.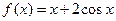 在
在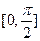 取最大值时,
取最大值时,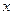 的值为_________
的值为_________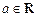 ,若函数
,若函数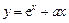 ,
,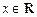 ,有大于零的极值点,则
,有大于零的极值点,则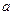 的取值范
的取值范 围是 .
围是 .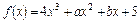 的图象在
的图象在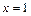 处的切线方程为
处的切线方程为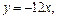
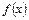 的解析式;
的解析式;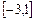 上的最值。
上的最值。