Question

【题目】已知圆经过原点且与直线相切于点

（Ⅰ）求圆的方程；

（Ⅱ）在圆上是否存在两点关于直线对称，且以线段为直径的圆经过原点？若存在,写出直线的方程；若不存在，请说明理由

Answer 1

【答案】（Ⅰ）.

（Ⅱ）见解析.

【解析】

（Ⅰ）由已知得圆心经过点P（4，0）、且与y=2x﹣8垂直的直线上，它又在线段OP的中垂线x=2上，求得圆心C（2，1），半径为，可得圆C的方程．

（Ⅱ）假设存在两点M，N关于直线y=kx﹣1对称，则y=kx﹣1通过圆心C（2，1），求得k=1，设直线MN为y=﹣x+b，代入圆的方程，利用韦达定理及 =0，求得b的值，可得结论．

（Ⅰ）法一：由已知，得圆心在经过点且与垂直的直线上，它又在线段的中垂线上，所以求得圆心，半径为.

所以圆的方程为.

(细则：法一中圆心3分，半径1分，方程2分)

法二：设圆的方程为，

可得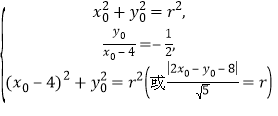

解得,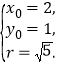

所以圆的方程为

(细则：方程组中一个方程1分)

（Ⅱ）假设存在两点关于直线对称，则通过圆心，求得，

所以设直线为

代入圆的方程得，

设，，则

解得或

这时，符合题意，所以存在直线为或符合条件

(细则：未判断的扣1分).