Question

8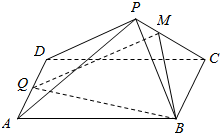．如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，Q为AD的中点，点M在线段PC上且PM=tPC（t＞0），试确定实数t的值，使得PA∥平面MQB．

Answer 1

分析 连AC交BQ于N，交BD于O，点M在线段PC上，PM=tPC，实数t=$\frac{1}{3}$的值，由PA∥平面MQB，利用PA∥MN，说明三角形相似，求出t=$\frac{1}{3}$．

解答 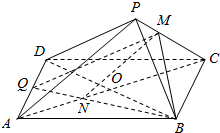解：当t=$\frac{1}{3}$时，使得PA∥平面MQB．
连AC交BQ于N，交BD于O，
则O为BD的中点，又∵BQ为△ABD边AD上中线，
∴N为三角形ABD的重心，可得：$\frac{AN}{NO}=2$，$\frac{AN}{AC}=\frac{1}{3}$，
∴PA∥平面MQB，PA?平面PAC，平面PAC∩平面MQB=MN，
∴PA∥MN，
$\frac{PM}{PC}$=$\frac{AN}{AC}$=$\frac{1}{3}$即：PM=$\frac{1}{3}$PC，t=$\frac{1}{3}$．

点评 本题主要考查了直线与平面平行的判定，考查了空间想象能力，逻辑思维能力以及推理论证能力，属于中档题．