题目内容
3.已知数列{an}是递增的等比数列,a1+a4=9,a2a3=8.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=an•log2an,求数列{bn}的前n项和Tn.
分析 (Ⅰ)运用等比数列的通项公式,可得方程组,求得首项和公差,即可得到所求通项公式;
(Ⅱ)运用对数的运算性质,化简bn,再由数列的求和方法:错位相减法,结合等比数列的求和公式即可得到.
解答 解法一:(Ⅰ)由$\left\{\begin{array}{l}{a_1}+{a_4}=9\\{a_2}{a_3}=8\end{array}\right.$即$\left\{\begin{array}{l}{a_1}+{a_1}{q^3}=9\\{a_1}^2{q^3}=8\end{array}\right.$,
消q3得${a_1}+\frac{8}{a_1}=9$,解得a1=1或a1=8,
∴$\left\{\begin{array}{l}{a_1}=1\\ q=2\end{array}\right.$或$\left\{\begin{array}{l}{a_1}=8\\ q=\frac{1}{2}\end{array}\right.$,
∵{an}是递增数列,∴$\left\{\begin{array}{l}{a_1}=1\\ q=2\end{array}\right.$,
∴${a_n}={a_1}{q^{n-1}}={2^{n-1}}$;
(Ⅱ)${b_n}={2^{n-1}}{log_2}{2^{n-1}}=(n-1)•{2^{n-1}}$,
${T_n}=0•{2^0}+1•{2^1}+2•{2^2}+…+(n-1)•{2^{n-1}}$,
2Tn=0•21+1•22+2•23+…+(n-2)•2n-1+(n-1)•2n,
∴相减可得,$-{T_n}={2^1}+{2^2}+…+{2^{n-1}}-(n-1)•{2^n}$=$\frac{{2-{2^n}}}{1-2}-(n-1)•{2^n}$
=(2-n)•2n-2,
∴${T_n}=(n-2)•{2^n}+2$.
解法二:(Ⅰ)因为{an}是等比数列,a2a3=8,所以a1a4=8.
又∵a1+a4=9,∴a1,a4是方程x2-9x+8=0的两根,
∴$\left\{\begin{array}{l}{a_1}=1\\{a_4}=8\end{array}\right.$或$\left\{\begin{array}{l}{a_1}=8\\{a_4}=1\end{array}\right.$.
∵{an}是递增数列,∴$\left\{\begin{array}{l}{a_1}=1\\{a_4}=8\end{array}\right.$.
∴${q^3}=\frac{a_4}{a_1}=8$,∴q=2.∴${a_n}={a_1}{q^{n-1}}={2^{n-1}}$.
(Ⅱ)下同解法一.
点评 本题考查等比数列的通项公式和求和公式的运用,注意运用方程的思想,考查数列的求和方法:错位相减求和,考查运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $-\frac{7\sqrt{10}}{10}$ | D. | $-\frac{\sqrt{10}}{2}$ |
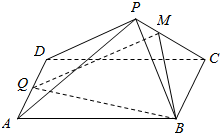 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,Q为AD的中点,点M在线段PC上且PM=tPC(t>0),试确定实数t的值,使得PA∥平面MQB.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,Q为AD的中点,点M在线段PC上且PM=tPC(t>0),试确定实数t的值,使得PA∥平面MQB.