题目内容
20.已知f(x)是定义在(-∞,0)∪(0,+∞)的奇函数,当x∈(-∞,0)时,f(x)=x2+2x,那么当x∈(0,+∞)时,f(x)=-x2+2x.分析 设x>0,则-x<0,运用已知解析式和奇函数的定义,即可得到所求的解析式.
解答 解:设x>0,则-x<0,
由于当x∈(-∞,0)时,f(x)=x2+2x,
即有f(-x)=x2-2x,
又f(x)为奇函数,则f(-x)=-f(x),
即有-f(x)=x2-2x,
即f(x)=-x2+2x.
故答案为:-x2+2x.
点评 本题考查函数的奇偶性的运用:求解析式,注意奇偶函数的定义的运用,考查运算能力,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
5.已知P(2$\sqrt{2}$,$\sqrt{5}$)在双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{{b}^{2}}$=1上,其左、右焦点分别为F1、F2,三角形PF1F2的内切圆切x轴于点M,则$\overrightarrow{MP}$•$\overrightarrow{M{F}_{2}}$的值为( )
| A. | 2$\sqrt{2}$-1 | B. | 2$\sqrt{2}$+1 | C. | 2$\sqrt{2}$-2 | D. | 2$\sqrt{2}$-$\sqrt{5}$ |
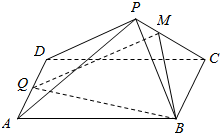 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,Q为AD的中点,点M在线段PC上且PM=tPC(t>0),试确定实数t的值,使得PA∥平面MQB.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,Q为AD的中点,点M在线段PC上且PM=tPC(t>0),试确定实数t的值,使得PA∥平面MQB. 设函数f(x)=|x2-2x-8|.
设函数f(x)=|x2-2x-8|.