题目内容
13.在数列{an}中,a1=1,an=$\frac{{{a_{n-1}}}}{{c{a_{n-1}}+1}}$(c为常数,n∈N*,n≥2),又a1,a2,a5成公比不为l的等比数列.(I)求证:{$\frac{1}{a_n}$}为等差数列,并求c的值;
(Ⅱ)设{bn}满足b1=$\frac{2}{3}$,bn=an-1an+1(n≥2,n∈N*),求数列{bn}的前n项和Sn.
分析 (Ⅰ)由题意可得 an≠0,化简条件可得$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$=c,可得{$\frac{1}{{a}_{n}}$}为等差数列,由等差数列的定义求出{$\frac{1}{{a}_{n}}$}的通项公式,由 a22=a1a5 解得c的值;
(Ⅱ)先求出{bn}的通项公式为bn=$\frac{1}{(2n-3)(2n+1)}$(n≥2),用裂项法求出{bn}的前n项和sn.
解答 解:(Ⅰ)证明:由题意可得 an≠0.否则,若存在an=0(n>1).
由递增式必有an-1=0,从而导致a1=0,这与a1=1矛盾.
∴$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$=c,故{$\frac{1}{{a}_{n}}$}是以c为公差,$\frac{1}{{a}_{1}}$=1为首项的等差数列.
故$\frac{1}{{a}_{n}}$=1+(n-1)c,∴an=$\frac{1}{1+(n-1)c}$.
从而a2=$\frac{1}{1+c}$,a5=$\frac{1}{1+4c}$,
由 a22=a1a5 解得c=2或c=0.
当c=0时,a1=a2=a5,舍去.故取c=2.
(Ⅱ)an=$\frac{1}{2n-1}$,故对{bn}:b1=$\frac{2}{3}$,
bn=$\frac{1}{(2n-3)(2n+1)}$(n≥2),
Sn=b1+b2+b3+…+bn,
当n≥2时,Sn=$\frac{2}{3}$+$\frac{1}{4}$[(1-$\frac{1}{5}$)+($\frac{1}{3}$-$\frac{1}{7}$)+($\frac{1}{5}$-$\frac{1}{9}$)
+($\frac{1}{7}$-$\frac{1}{11}$)+…+($\frac{1}{2n-5}$-$\frac{1}{2n-1}$)+($\frac{1}{2n-3}$-$\frac{1}{2n+1}$)
=$\frac{2}{3}$+$\frac{1}{4}$(1+$\frac{1}{3}$-$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)=1-$\frac{1}{4}$($\frac{1}{2n-1}$+$\frac{1}{2n+1}$)
=1-$\frac{n}{4{n}^{2}-1}$.
当n=1时,$1-\frac{n}{{4{n^2}-1}}=\frac{2}{3}$,
所以${S_n}=1-\frac{n}{{4{n^2}-1}}(n∈{N^*})$.
点评 本题主要考查等差数列、等比数列的定义和性质,求等差数列的通项公式,用裂项法对数列进行求和,求出Sn的值,是解题的难点,属于中档题.

| A. | f(x)=x3 | B. | f(x)=x2 | C. | f(x)=4x-x2 | D. | f(x)=$\left\{\begin{array}{l}{-1,x≥0}\\{1,x<0}\end{array}\right.$ |
| A. | g(x1)<0,f(x2)>0 | B. | g(x1)>0,f(x2)<0 | C. | g(x1)>0,f(x2)>0 | D. | g(x1)<0,f(x2)<0 |
| A. | 2$\sqrt{2}$-1 | B. | 2$\sqrt{2}$+1 | C. | 2$\sqrt{2}$-2 | D. | 2$\sqrt{2}$-$\sqrt{5}$ |
| A. | m=-1 | B. | m=-2 | C. | m=-1或2 | D. | m=l或m=-2 |
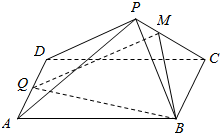 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,Q为AD的中点,点M在线段PC上且PM=tPC(t>0),试确定实数t的值,使得PA∥平面MQB.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,Q为AD的中点,点M在线段PC上且PM=tPC(t>0),试确定实数t的值,使得PA∥平面MQB.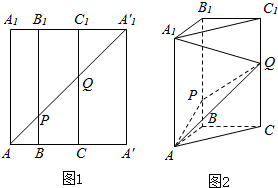 如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA1′分别交BB1,CC1于点P,Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1中
如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA1′分别交BB1,CC1于点P,Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1中