题目内容
16.在△ABC中,a,b,c分别是三个内角A,B,C的对边,设向量$\overrightarrow{p}$=(b-c,a-c),$\overrightarrow{q}$=(c+a,b),若$\overrightarrow{p}$∥$\overrightarrow{q}$,则角A的大小是( )| A. | 90° | B. | 45° | C. | 60° | D. | 30° |
分析 利用向量共线,推出三角形的边长关系,利用余弦定理求解A的大小.
解答 解:在△ABC中,a,b,c分别是三个内角A,B,C的对边,设向量$\overrightarrow{p}$=(b-c,a-c),$\overrightarrow{q}$=(c+a,b),若$\overrightarrow{p}$∥$\overrightarrow{q}$,可得(a-c)(a+c)=(b-c)b,即a2-c2=b2-bc,
可得cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}=\frac{1}{2}$,
A=60°.
故选:C.
点评 本题考查斜率的共线的充要条件,余弦定理的应用,考查计算能力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5.一个物体的运动方程为s=1-t+t2,其中s的单位是m,t的单位是s,那么物体在最初3s内的平均速度是( )
| A. | 7m/s | B. | 6m/s | C. | 2m/s | D. | 1m/s |
4.下列函数求值算法中需要条件语句的函数是( )
| A. | f(x)=x3 | B. | f(x)=x2 | C. | f(x)=4x-x2 | D. | f(x)=$\left\{\begin{array}{l}{-1,x≥0}\\{1,x<0}\end{array}\right.$ |
1.设函数f(x)=ex+x-2的零点为x1,函数g(x)=lnx+x2-3的零点为x2,则( )
| A. | g(x1)<0,f(x2)>0 | B. | g(x1)>0,f(x2)<0 | C. | g(x1)>0,f(x2)>0 | D. | g(x1)<0,f(x2)<0 |
5.已知P(2$\sqrt{2}$,$\sqrt{5}$)在双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{{b}^{2}}$=1上,其左、右焦点分别为F1、F2,三角形PF1F2的内切圆切x轴于点M,则$\overrightarrow{MP}$•$\overrightarrow{M{F}_{2}}$的值为( )
| A. | 2$\sqrt{2}$-1 | B. | 2$\sqrt{2}$+1 | C. | 2$\sqrt{2}$-2 | D. | 2$\sqrt{2}$-$\sqrt{5}$ |
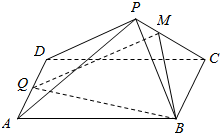 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,Q为AD的中点,点M在线段PC上且PM=tPC(t>0),试确定实数t的值,使得PA∥平面MQB.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,Q为AD的中点,点M在线段PC上且PM=tPC(t>0),试确定实数t的值,使得PA∥平面MQB.