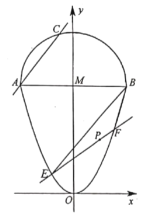
题目内容
【题目】设![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左,右焦点,
的左,右焦点,![]() 两点分别是椭圆
两点分别是椭圆![]() 的上,下顶点,
的上,下顶点,![]() 是等腰直角三角形,延长
是等腰直角三角形,延长![]() 交椭圆
交椭圆![]() 于
于![]() 点,且
点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的动点,直线
的动点,直线![]() 与直
与直![]() 分别相交于
分别相交于![]() 两点,点
两点,点![]() ,试问:
,试问:![]() 的外接圆是否恒过
的外接圆是否恒过![]() 轴上的定点(异于点
轴上的定点(异于点![]() )?若是,求该定点坐标;若否,请说明理由.
)?若是,求该定点坐标;若否,请说明理由.
【答案】(1)![]() ;(2)是,
;(2)是,![]()
【解析】
(1)利用椭圆的定义可得![]() ,结合
,结合![]() 是等腰直角三角形,可求椭圆的方程;
是等腰直角三角形,可求椭圆的方程;
(2)设出直线方程,表示出![]() 的坐标,求出圆心,利用半径相等可得定点坐标.
的坐标,求出圆心,利用半径相等可得定点坐标.
(1)∵![]() 的周长为
的周长为![]() ,由定义可知,
,由定义可知,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又∵![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,∴
,∴![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() ;
;
(2)设![]() ,则
,则![]() ,
,
∴直线![]() 与
与![]() 的斜率之积为
的斜率之积为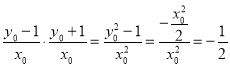 ,
,
设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() ,
,![]() ,
,
由![]() ,可得
,可得![]() ,同理
,同理![]() ,
,
假设![]() 的外接圆恒过定点了
的外接圆恒过定点了![]() ,
,
则其圆心![]() ,
,
又![]()
∴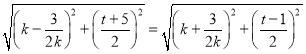 ,
,
∴解得![]() ,
,
∴![]() 的外接圆恒过
的外接圆恒过![]() 轴定点
轴定点![]() .
.

练习册系列答案
相关题目
【题目】为考察高中生的性别与是否喜欢数学课程之间的关系,某校在高中生中随机抽取100名学生进行了问卷调查,得到如下列联表:
喜欢数学 | 不喜欢数学 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 50 | 100 |
(1)请将上面的列联表补充完整;
(2)能否在犯错误的概率不超过0.001的前提下认为“喜欢数学”与性别有关?说明你的理由;
(3)若在接受调查的所有男生中按照“是否喜欢数学”进行分层抽样,现随机抽取6人,再从6人中抽取3人,求至少有1人“不喜欢数学”的概率.
下面的临界值表供参考:
| 0.05 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式: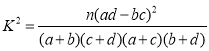 ,其中
,其中![]() ).
).