题目内容
【题目】设f（x）＝|lnx|，若函数g（x）＝f（x）-ax在区间（0，4）上有三个零点，则实数a的取值范围是（ ）
A. （0，
）B. （
，e）C. （，）D. （0，）
【答案】C
【解析】
函数g（x）＝f（x）-ax在区间（0，4）上有三个零点等价于|lnx|-ax＝0在区间（0，4）上有三个不同的解，分离参数后等价于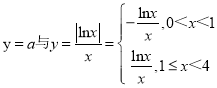
函数图像有三个交点，通过
的图像较容易求处实数a的取值范围。
∵g（x）＝f（x）-ax在区间（0，4）上有三个零点，
∴|lnx|-ax＝0在区间（0，4）上有三个不同的解，
令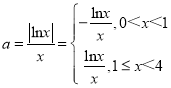
；
则当0＜x＜1时，
的值域为（0，+∞）；
当1≤x＜4时，
在[1，e]上是增函数，
，在[e，4）上是减函数，
；故当
时，有三个不同的解.
故选：C.
阅读快车系列答案
【题目】平顶山市公安局交警支队依据《中华人民共和国道路交通安全法》第
条规定：所有主干道路凡机动车途经十字口或斑马线，无论转弯或者直行，遇有行人过马路，必须礼让行人，违反者将被处以
元罚款，记
分的行政处罚．如表是本市一主干路段监控设备所抓拍的
个月内，机动车驾驶员不“礼让斑马线”行为统计数据：
月份 |
|
|
|
|
|
违章驾驶员人数 |
|
|
|
|
|
（Ⅰ）请利用所给数据求违章人数
与月份
之间的回归直线方程
；
（Ⅱ）预测该路段
月份的不“礼让斑马线”违章驾驶员人数．
参考公式：
，
．
【题目】某工厂的某车间共有
位工人，其中
的人爱好运动。经体检调查，这位工人的健康指数（百分制）如下茎叶图所示。体检评价标准指出：健康指数不低于
者为“身体状况好”，健康指数低于者为“身体状况一般”。
（1）根据以上资料完成下面的
列联表，并判断有多大把握认为“身体状况好与爱好运动有关系”？
身体状况好 | 身体状况一般 | 总计 | |
爱好运动 | |||
不爱好运动 | |||
总计 |
|
（2）现将位工人的健康指数分为如下
组：
，
，
，
，
，其频率分布直方图如图所示。计算该车间中工人的健康指数的平均数，由茎叶图得到真实值记为
，由频率分布直方图得到估计值记为
，求与的误差值；
（3）以该车间的样本数据来估计该厂的总体数据，若从该厂健康指数不低于者中任选
人，设
表示爱好运动的人数，求的数学期望。
附：
。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
