Question

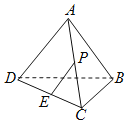
【题目】已知三棱锥A﹣BCD的所有棱长均相等，E为DC的中点，若点P为AC中点，则直线PE与平面BCD所成角的正弦值为_____，若点Q在棱AC所在直线上运动，则直线QE与平面BCD所成角正弦值的最大值为_____．

Answer 1

【答案】

【解析】

，则直线PE与平面BCD所成角等于直线与平面BCD所成角，过A作AO⊥底面BCD，垂足为O，连结OD，则∠ADO是直线PE与平面BCD所成角，在中求解即得，是一个正四面体，当Q与A重合时，直线QE与平面BCD所成角正弦值取最大值，在中计算可得最大值．

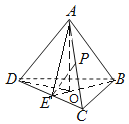
连结BE，AE，过A作AO⊥底面BCD，垂足为O，连结OD，

则∠ADO是直线PE与平面BCD所成角，

设三棱锥A﹣BCD的所有棱长均相等，设棱长为2，

则DO＝BOBE，

AO，

∴sin∠ADO．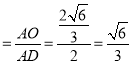

∴直线PE与平面BCD所成角的正弦值为．

当Q与A重合时，直线QE与平面BCD所成角正弦值取最大值，

此时直线QE与平面BCD所成角为∠AEO，AE，

∴直线QE与平面BCD所成角正弦值的最大值为：

sin∠AEO．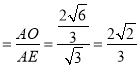

故答案为：，