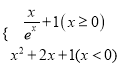题目内容
【题目】已知椭圆![]() 与x轴负半轴交于
与x轴负半轴交于![]() ,离心率
,离心率![]() .
.
(1)求椭圆C的方程;
(2)设直线![]() 与椭圆C交于
与椭圆C交于![]() 两点,连接AM,AN并延长交直线x=4于
两点,连接AM,AN并延长交直线x=4于![]() 两点,若
两点,若![]() ,直线MN是否恒过定点,如果是,请求出定点坐标,如果不是,请说明理由.
,直线MN是否恒过定点,如果是,请求出定点坐标,如果不是,请说明理由.
【答案】(1)![]() (2)直线
(2)直线![]() 恒过定点
恒过定点![]() ,详见解析
,详见解析
【解析】
(1)依题意由椭圆的简单性质可求出![]() ,即得椭圆C的方程;
,即得椭圆C的方程;
(2)设直线![]() 的方程为:
的方程为:![]() ,联立直线
,联立直线![]() 的方程与椭圆方程可求得点
的方程与椭圆方程可求得点![]() 的坐标,同理可求出点
的坐标,同理可求出点![]() 的坐标,根据
的坐标,根据![]() 的坐标可求出直线
的坐标可求出直线![]() 的方程,将其化简成点斜式,即可求出定点坐标.
的方程,将其化简成点斜式,即可求出定点坐标.
(1)由题有![]() ,
,![]() .∴
.∴![]() ,∴
,∴![]() .∴椭圆方程为
.∴椭圆方程为![]() .
.
(2)设直线![]() 的方程为:
的方程为:![]() ,则
,则
∴![]() 或
或![]() ,∴
,∴![]() ,同理
,同理![]() ,
,![]()
当![]() 时,由
时,由![]() 有
有![]() .∴
.∴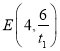 ,同理
,同理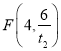 ,又
,又![]()
∴![]() ,
,![]()
当![]() 时,
时,![]() ∴直线
∴直线![]() 的方程为
的方程为![]()
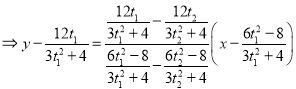
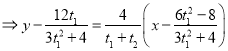
![]()
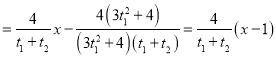
∴直线![]() 恒过定点
恒过定点![]() ,当
,当![]() 时,此时也过定点
时,此时也过定点![]() ..
..
综上:直线![]() 恒过定点
恒过定点![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目