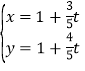题目内容
【题目】已知函数![]() ,给出下列命题,其中正确命题的个数为
,给出下列命题,其中正确命题的个数为
①当![]() 时,
时,![]() 上单调递增;
上单调递增;
②当![]() 时,存在不相等的两个实数
时,存在不相等的两个实数![]() ,使
,使![]() ;
;
③当![]() 时,
时,![]() 有3个零点.
有3个零点.
A. 3B. 2C. 1D. 0
【答案】C
【解析】
①![]() 时,判断
时,判断![]() 在
在![]() 的单调性;
的单调性;
②![]() ,分别求
,分别求![]() 与
与![]() 的函数值的范围,判断是否有交集;
的函数值的范围,判断是否有交集;
③令![]() ,
,![]() 时
时![]() 有一解;
有一解;![]() 时利用一元二次方程根的分别条件判断方程
时利用一元二次方程根的分别条件判断方程![]() ,即
,即![]() 在
在![]() 是否有两解.
是否有两解.
记![]() ,
,![]() .
.
当![]() 时,对称轴
时,对称轴![]() ,
,
知函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
又因为![]() 在区间
在区间![]() 单调递增,(如图一)
单调递增,(如图一)
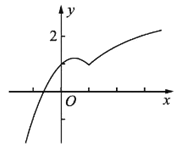
所以选项①错误.
当![]() 时,对称轴
时,对称轴![]() ,
,
知函数![]() 在
在![]() 单调递增,
单调递增,![]() 在区间
在区间![]() 单调递增.
单调递增.
从而![]() 在
在![]() 单调递增(如图二),
单调递增(如图二),
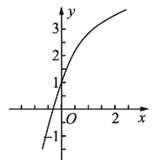
所以选项②错误;
对于③,当![]() 时,
时,
对称轴![]() ,
,
所以![]() 在
在![]() 单调递增;在
单调递增;在![]() 单调递减;
单调递减;
![]() 在区间
在区间![]() 单调递增,
单调递增,
且有![]() ,
,![]() ,
,
所以函数![]() 的图象与
的图象与![]() 轴有3个交点(如图示),
轴有3个交点(如图示),
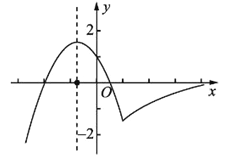
所以③正确,综合可知正确选项只有一个.
选项C正确.

练习册系列答案
相关题目
【题目】为了调查民众对国家实行“新农村建设”政策的态度,现通过网络问卷随机调查了年龄在20周岁至80周岁的100人,他们年龄频数分布和支持“新农村建设”人数如下表:
年龄 |
|
|
|
|
|
|
频数 | 10 | 20 | 30 | 20 | 10 | 10 |
支持“新农村建设” | 3 | 11 | 26 | 12 | 6 | 2 |
(1)根据上述统计数据填下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为以50岁为分界点对“新农村建设”政策的支持度有差异;
的把握认为以50岁为分界点对“新农村建设”政策的支持度有差异;
年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
支持 | |||
不支持 | |||
合计 |
(2)现从年龄在![]() 内的5名被调查人中任选两人去参加座谈会,求选出两人中恰有一人支持新农村建设的概率.
内的5名被调查人中任选两人去参加座谈会,求选出两人中恰有一人支持新农村建设的概率.
参考数据:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]() .
.