Question

【题目】在直角坐标系xOy中，以O为极点，x正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρcos（θ﹣ ）=1，A，B分别为C与x轴，y轴的交点．
（1）写出C的直角坐标方程，并求A，B的极坐标；
（2）设M为曲线C上的一个动点， =λ （λ＞0），| || |=2，求动点Q的极坐标方程．

Answer 1

【答案】
（1）解：由曲线C的极坐标方程为ρcos（θ﹣ ）=1，展开为 + ρsinθ=1，可得直线C的直角坐标方程为 x+ y=1，即x+ y=2．

当θ=0时，ρ=2，∴A（2，0）；

当θ= 时，ρ= ，∴B

（2）解：由条件可设Q（ρ，θ）， ，

由条件 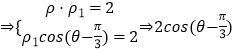为所求Q的极坐标方程

【解析】（1）由曲线C的极坐标方程为ρcos（θ﹣ ）=1，展开为 + ρsinθ=1，利用互化公式可得直线C的直角坐标方程，分别取θ=0，θ= 时，计算出ρ，即可得出直角坐标．（2）由条件可设Q（ρ，θ） ，由已知可得ρρ1=2， =2，联立解出ρj即可得出方程．