Question

【题目】已知函数f（x）=ln（ax+1）+ ﹣x2﹣ax（a∈R）
（1）若y=f（x）在[4，+∞）上为增函数，求实数a的取值范围；
（2）当a≥ 时，设g（x）=ln[x2（ax+1）]+ ﹣3ax﹣f（x）（x＞0）的两个极值点x1 ， x2（x1＜x2）恰为φ（x）=lnx﹣cx2﹣bx的零点，求y=（x1﹣x2）φ′（ ）的最小值．

Answer 1

【答案】
（1）解：由题意f′（x）= +x2﹣2x﹣a≥0在[4，+∞）上恒成立，

整理得ax2+（1﹣2a）x﹣a2﹣2≥0在[4，+∞）上恒成立

设h（x）=ax2+（1﹣2a）x﹣a2﹣2，显然a＞0其对称轴为x=1﹣ ＜1

∴h（x）在[4，+∞）单调递增，∴只要h（4）=16a+4（1﹣2a）﹣a2﹣2≥0，

∴0＜a≤4+3

（2）解：g（x）=2lnx﹣2ax+x2，g′（x）= ．

由题意 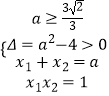，∴ ≥ ，解得0＜ ≤ ，

φ′（x）= ﹣2cx﹣b，φ（x1）=lnx1﹣cx12﹣bx1，φ（x2）=lnx2﹣cx22﹣bx2，

两式相减得ln ﹣c（x1﹣x2）（x1+x2）﹣b（x1﹣x2）=0，

∴y=（x1﹣x2）φ′（ ）= ﹣lnt（0＜t≤ ），

∴y′= ＜0．

∴y=（x1﹣x2）φ′（ ）在（0， ]递减，ymin=ln2﹣ ．

∴y=（x1﹣x2）φ′（ ）的最小值为ln2﹣

【解析】（1）由题意f′（x）= +x2﹣2x﹣a≥0在[4，+∞）上恒成立，整理得ax2+（1﹣2a）x﹣a2﹣2≥0在[4，+∞）上恒成立，设h（x）=ax2+（1﹣2a）x﹣a2﹣2，只要h（4）=16a+4（1﹣2a）﹣a2﹣2≥0，即可求实数a的取值范围；（2）先确定0＜ ≤ ，再利用y=（x1﹣x2）φ′（ ）= ﹣lnt（0＜t≤ ），即可求y=（x1﹣x2）φ′（ ）的最小值．
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的极值与导数，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减；求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值即可以解答此题．