Question

【题目】设函数f（x）=|3x﹣1|+ax+3．
（1）若a=1，解不等式f（x）≤5；
（2）若函数f（x）有最小值，求实数a的取值范围．

Answer 1

【答案】
（1）解：a=1时，f（x）=|3x﹣1|+x+3．

当 时，f（x）≤5可化为3x﹣1+x+3≤5，解之得 ；

当 时，f（x）≤5可化为﹣3x+1+x+3≤5，解之得 ．

综上可得，原不等式的解集为 ．

（2）解：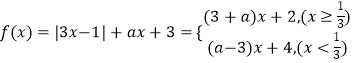

函数f（x）有最小值的充要条件为 ，即﹣3≤a≤3．

【解析】（1）a=1时，f（x）=|3x﹣1|+x+3，分类讨论，去掉绝对值，求得x的范围．（2）化简f（x）的解析式，根据一次函数的单调性与一次项系数符号的关系，求得a的范围．
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识，掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值，以及对绝对值不等式的解法的理解，了解含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号．