题目内容
【题目】过点![]() 作圆
作圆![]()
![]() 的切线,
的切线, ![]() 为坐标原点,切点为
为坐标原点,切点为![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() 是圆
是圆![]() 上位于第一象限内的任意一点,过点
上位于第一象限内的任意一点,过点![]() 作圆
作圆![]() 的切线
的切线![]() ,且
,且![]() 交
交![]() 轴于点
轴于点![]() ,交y轴于点
,交y轴于点![]() ,设
,设![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)4;(2)8
【解析】试题分析:首先利用圆的弦长公式,求出圆的半径;涉及到直线与两坐标轴的交点问题大多采用线方程的截距式,但务必要检验,设直线方程的截距式,由于直线与圆相切于第一象限,满足相切条件,且截距均为正,利用均值不等式进行“等转不等”,得出向量OQ的模的最小值.
试题解析:
(1)圆![]()
![]() 的圆心为
的圆心为![]() ,于是
,于是![]() ,由题设知,
,由题设知, ![]() 是以
是以![]() 为直角顶点的直角三角形,故有
为直角顶点的直角三角形,故有![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,则
,则![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() .∵直线
.∵直线![]() 与圆
与圆![]() 相切,∴
相切,∴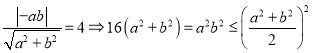 ,∴
,∴![]() ∴
∴![]() ,当且仅当
,当且仅当![]() 时取到“=”,∴
时取到“=”,∴![]() 取得最小值为8.
取得最小值为8.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
