题目内容
【题目】已知函数![]() (a为实数).
(a为实数).
(1) 若函数![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行,求实数a的值;
平行,求实数a的值;
(2) 若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(3) 若函数![]() 在区间
在区间![]() 上是增函数,求a的取值范围.
上是增函数,求a的取值范围.
【答案】(1) ![]() (2)
(2)![]() (3)
(3)![]() .
.
【解析】试题分析:(1)由导数几何意义得切线斜率为![]() 得方程,解得实数a的值;(2)先求导数,再求导函数零点,列表分析导函数符号变化规律,确定单调性,进而确定最值与值域(3)转化为
得方程,解得实数a的值;(2)先求导数,再求导函数零点,列表分析导函数符号变化规律,确定单调性,进而确定最值与值域(3)转化为![]()
![]()
![]() 对于1≤
对于1≤![]() ≤3恒成立,再分离变量得
≤3恒成立,再分离变量得![]() 最大值,最后根据函数最值得
最大值,最后根据函数最值得![]() 的取值范围
的取值范围
试题解析:(1) ![]() ,
, ![]() ,解得
,解得![]() .
.
(2)![]() 时,
时, ![]() ,
,
![]() ,令
,令![]() ,解得
,解得![]() 或
或![]() ,
,
|
| 2 |
|
| — | 0 | + |
| 减函数 | 极小值 | 增函数 |
又![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 上的值域为
上的值域为![]() .
.
(3)![]() ,由
,由![]() 在区间
在区间![]() 上是增函数,
上是增函数,
则![]()
![]()
![]() 对于1≤
对于1≤![]() ≤3恒成立,所以
≤3恒成立,所以![]() .
.
因![]() ,故
,故![]() ,记
,记![]() ,则
,则![]() ,
,
而函数![]() 在
在![]() 上为减函数,则
上为减函数,则![]() ,所以
,所以![]()
![]() 4.
4.
所以![]() 的取值范围是
的取值范围是![]() .
.

 快捷英语周周练系列答案
快捷英语周周练系列答案【题目】学校从参加高一年级期中考试的学生中抽出![]() 名学生,并统计了她们的数学成绩(成绩均为整数且满分为
名学生,并统计了她们的数学成绩(成绩均为整数且满分为![]() 分),数学成绩分组及各组频数如下:
分),数学成绩分组及各组频数如下:
![]()
样本频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)在给出的样本频率分布表中,求![]() 的值;
的值;
(2)估计成绩在![]() 分以上(含
分以上(含![]() 分)学生的比例;
分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在![]() 的学生中选两位同学,共同帮助成绩在
的学生中选两位同学,共同帮助成绩在![]() 中的某一位同学.已知甲同学的成绩为
中的某一位同学.已知甲同学的成绩为![]() 分,乙同学的成绩为
分,乙同学的成绩为![]() 分,求甲、乙两同学恰好被安排在同一小组的概率.
分,求甲、乙两同学恰好被安排在同一小组的概率.
【题目】为响应党中央“扶贫攻坚”的号召,某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高,根据以往的经验,随着温度的升高,其死亡株数成增长的趋势.下表给出了2018年种植的一批试验紫甘薯在不同温度时6组死亡的株数:
温度 | 21 | 23 | 24 | 27 | 29 | 32 |
死亡数 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算:![]() ,
,![]() ,
,![]() ,
,![]() .
.
其中![]() 分别为试验数据中的温度和死亡株数,
分别为试验数据中的温度和死亡株数,![]() .
.
(1)![]() 与
与![]() 是否有较强的线性相关性? 请计算相关系数
是否有较强的线性相关性? 请计算相关系数![]() (精确到
(精确到![]() )说明.
)说明.
(2)并求![]() 关于
关于![]() 的回归方程
的回归方程![]() (
(![]() 和
和![]() 都精确到
都精确到![]() );
);
(3)用(2)中的线性回归模型预测温度为![]() 时该批紫甘薯死亡株数(结果取整数).
时该批紫甘薯死亡株数(结果取整数).
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,
,
①线性相关系数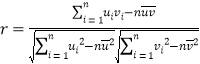 ,通常情况下当
,通常情况下当![]() 大于0.8时,认为两
大于0.8时,认为两
个变量有很强的线性相关性.
②其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
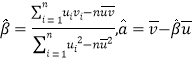 ;
;

