题目内容
【题目】在下列命题中:
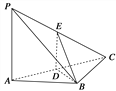
①若向量a,b共线,则向量a,b所在的直线平行;
②若向量a,b所在的直线为异面直线,则向量a,b一定不共面;
③若三个向量a,b,c两两共面,则向量a,b,c共面;
④已知空间的三个向量![]() ,则对于空间的任意一个向量
,则对于空间的任意一个向量![]() ,总存在实数x,y,z,使得
,总存在实数x,y,z,使得![]() 。
。
正确命题的个数是( )
A. 0 B. 1 C. 2 D. 3
【答案】A
【解析】:①若向量![]() 共线,则向量
共线,则向量![]() 所在的直线平行,此命题不正确,同一直线上的两个向量也是共线的,此时两直线重合;
所在的直线平行,此命题不正确,同一直线上的两个向量也是共线的,此时两直线重合;
②若向量![]() 所在的直线为异面直线,则向量
所在的直线为异面直线,则向量![]() 不共面,此命题不正确,任意两两向量是共面的;
不共面,此命题不正确,任意两两向量是共面的;
③若三个向量![]() 两两共面,则向量
两两共面,则向量![]() 共面,此命题不正确,两两共面的三个向量不一定共面,三个不共面的向量也满足任意两个之间是共面的;
共面,此命题不正确,两两共面的三个向量不一定共面,三个不共面的向量也满足任意两个之间是共面的;
④已知空间不共面的三个向量![]() 则对于空间的任意一个向量
则对于空间的任意一个向量![]() 总存在实数x、y、z,使得
总存在实数x、y、z,使得![]() 此命题是正确的,它是空间向量共面定理;
此命题是正确的,它是空间向量共面定理;
综上讨论知,只有④是正确的
故选B

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
【题目】学校从参加高一年级期中考试的学生中抽出![]() 名学生,并统计了她们的数学成绩(成绩均为整数且满分为
名学生,并统计了她们的数学成绩(成绩均为整数且满分为![]() 分),数学成绩分组及各组频数如下:
分),数学成绩分组及各组频数如下:
![]()
样本频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)在给出的样本频率分布表中,求![]() 的值;
的值;
(2)估计成绩在![]() 分以上(含
分以上(含![]() 分)学生的比例;
分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在![]() 的学生中选两位同学,共同帮助成绩在
的学生中选两位同学,共同帮助成绩在![]() 中的某一位同学.已知甲同学的成绩为
中的某一位同学.已知甲同学的成绩为![]() 分,乙同学的成绩为
分,乙同学的成绩为![]() 分,求甲、乙两同学恰好被安排在同一小组的概率.
分,求甲、乙两同学恰好被安排在同一小组的概率.