题目内容
【题目】已知椭圆
： 
左焦点
，左顶点
，椭圆上一点
满足
轴，且点
在
轴下方， 
连线与左准线
交于点
，过点
任意引一直线与椭圆交于
，连结
交于点
，若实数
满足： 
， 
.
（1）求
的值；
（2）求证：点
在一定直线上.
【答案】（1）
（2）见解析
【解析】试题分析：
(1)由题意结合直线AB的方程为
，结合向量平行的充要条件比较系数可得
(2)设点
， 
， 
，联立直线与椭圆的方程，结合韦达定理有
， 
结合(1)的结论可得
，则点
在定直线
上.
试题解析：
（1）因为
，由
轴，由对称轴不妨设
，则直线
又左准线
，所以
，
又
，所以
同理：由
，得： 
又
，所以
又
，比较系数得： 
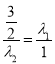，所以
（2）证明：设点
， 
， 
由
，得
， 
代入椭圆方程
，得：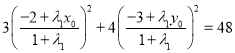 
，
整理得： 
显然
，所以
同理：由
，得： 
， 
代入椭圆方程
，得：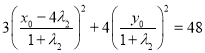 
同理可得： 
又由（1）
，所以
整理得： 
即点
在定直线
上.
第1卷单元月考期中期末系列答案
【题目】空气质量按照空气质量指数大小分为七档（五级），相对应空气质量的七个类别，指数越大，说明污染的情况越严重，对人体危害越大．
指数 | 级别 | 类别 | 户外活动建议 |
| Ⅰ | 优 | 可正常活动 |
| Ⅱ | 良 | |
| Ⅲ | 轻微污染 | 易感人群症状有轻度加剧，健康人群出现刺激症状，心脏病和呼吸系统疾病患者应减少体积消耗和户外活动． |
| 轻度污染 | ||
| Ⅳ | 中度污染 | 心脏病和肺病患者症状显著加剧，运动耐受力降低，健康人群中普遍出现症状，老年人和心脏病、肺病患者应减少体力活动． |
| 中度重污染 | ||
| Ⅴ | 重污染 | 健康人运动耐受力降低，由明显强烈症状，提前出现某些疾病，老年人和病人应当留在室内，避免体力消耗，一般人群应尽量减少户外活动． |
现统计邵阳市市区2016年1月至11月连续60天的空气质量指数，制成如图所示的频率分布直方图．
（1）求这60天中属轻度污染的天数；
（2）求这60天空气质量指数的平均值；
（3）将频率分布直方图中的五组从左到右依次命名为第一组，第二组，…，第五组．从第一组和第五组中的所有天数中抽出两天，记它们的空气质量指数分别为
， 
，求事件
的概率．
