题目内容
已知数列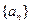 的前
的前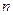 项和为
项和为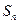 ,且
,且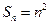 .数列
.数列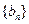 为等比数列,且
为等比数列,且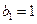 ,
,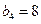 .
.
(Ⅰ)求数列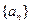 ,
,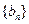 的通项公式;
的通项公式;
(Ⅱ)若数列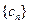 满足
满足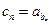 ,求数列
,求数列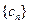 的前
的前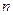 项和
项和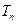 ;
;
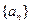 的前
的前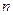 项和为
项和为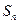 ,且
,且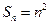 .数列
.数列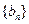 为等比数列,且
为等比数列,且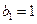 ,
,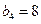 .
.(Ⅰ)求数列
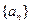 ,
,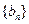 的通项公式;
的通项公式;(Ⅱ)若数列
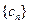 满足
满足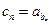 ,求数列
,求数列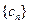 的前
的前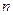 项和
项和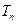 ;
;见解析
(Ⅰ)∵数列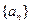 的前
的前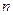 项和为
项和为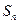 ,且
,且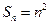 ,
,
∴当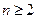 时,
时,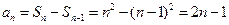 .
.
当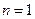 时,
时,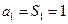 亦满足上式,故
亦满足上式,故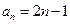 ,
,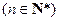 . ………………3分
. ………………3分
又数列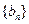 为等比数列,设公比为
为等比数列,设公比为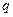 ,
,
∵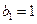 ,
,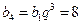 , ∴
, ∴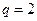 .
.
∴
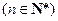 . …………6分
. …………6分
(Ⅱ)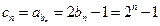 .
.
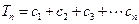
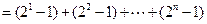
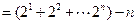
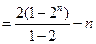 .
.
所以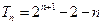 . ………………12分
. ………………12分
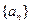 的前
的前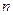 项和为
项和为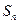 ,且
,且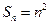 ,
,∴当
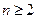 时,
时,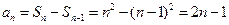 .
.当
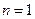 时,
时,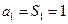 亦满足上式,故
亦满足上式,故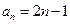 ,
,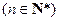 . ………………3分
. ………………3分又数列
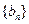 为等比数列,设公比为
为等比数列,设公比为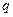 ,
,∵
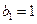 ,
,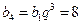 , ∴
, ∴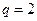 .
.∴

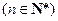 . …………6分
. …………6分(Ⅱ)
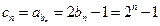 .
.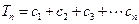
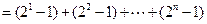
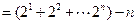
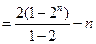 .
.所以
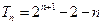 . ………………12分
. ………………12分
练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目

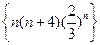 中的最大项是第
中的最大项是第 项,则
项,则 中,
中, ,点
,点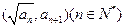 在函数
在函数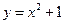 的图象上,数列
的图象上,数列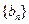 的前n项和
的前n项和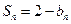 .
.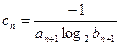 ,求
,求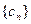 的前n项和
的前n项和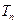 .
.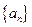 的前n项和为
的前n项和为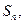 已知
已知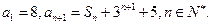
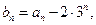 证明:数列
证明:数列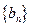 是等比数列;
是等比数列;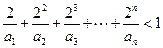 .
. ).
).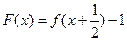 为R上的奇函数,
为R上的奇函数,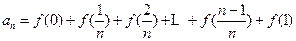
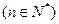 ,则数列
,则数列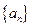 的通项公式为
的通项公式为



 [C1n d+2Cn2d2+…+(n—1)Cnn-1d n-1+nCnndn](n∈N*).
[C1n d+2Cn2d2+…+(n—1)Cnn-1d n-1+nCnndn](n∈N*).