题目内容
14．已知直线y=（3a-1）x+a-1，为使这条直线经过第一、三、四象限，则实数a的取值范围是$（\frac{1}{3}，1）$．分析 直线y=（3a-1）x+a-1，为使这条直线经过第一、三、四象限，可得$\left\{\begin{array}{l}{3a-1＞0}\\{a-1＜0}\end{array}\right.$，解得即可．
解答 解：∵直线y=（3a-1）x+a-1，为使这条直线经过第一、三、四象限，
∴$\left\{\begin{array}{l}{3a-1＞0}\\{a-1＜0}\end{array}\right.$，解得$\frac{1}{3}＜a＜1$．
故答案为：$（\frac{1}{3}，1）$．
点评 本题考查了直线的斜率与截距的应用，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
5．若点P在平面ABC内射影为O，且PA⊥BC，PB⊥AC，则点O为△ABC的（ ）
| A． | 重心 | B． | 外心 | C． | 内心 | D． | 垂心 |
2．已知函数f（x）=lnx+$\frac{2a}{x}$，a∈R
（1）若函数f（x）在[1，+∞）上是增函数，求实数a的取值范围；
（2）若函数f（x）在[1，e]上的最小值为2，求实数a的取值范围．
（1）若函数f（x）在[1，+∞）上是增函数，求实数a的取值范围；
（2）若函数f（x）在[1，e]上的最小值为2，求实数a的取值范围．
6．在△ABC中，a，b，c分别为角A，B，C所对的边，若acosA=bcosB，则此三角形一定是（ ）
| A． | 等腰直角三角形 | B． | 等腰或直角三角形 | ||
| C． | 等腰三角形 | D． | 直角三角形 |
3．已知a=$\frac{1}{n}$$\underset{\stackrel{n}{∑}}{i=1}$（$\frac{i}{n}$）2（n∈N*），b=${∫}_{0}^{1}$x2dx，则a，b的大小关系为（ ）
| A． | a＜b | B． | a=b | ||
| C． | a＞b | D． | a，b的大小与n的取值有关 |
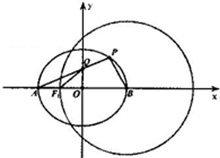如图，点A，B分别是椭圆E：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点，圆B：（x-2）2+y2=9，经过椭圆E的左焦点F．