题目内容
6.在△ABC中,a,b,c分别为角A,B,C所对的边,若acosA=bcosB,则此三角形一定是( )| A. | 等腰直角三角形 | B. | 等腰或直角三角形 | ||
| C. | 等腰三角形 | D. | 直角三角形 |
分析 由条件利用正弦定理可得 $\frac{1}{2}$sin2A=$\frac{1}{2}$sin2B,化简可得 A=B,或 A+B=$\frac{π}{2}$,故△ABC是等腰三角形或直角三角形,从而得出结论.
解答 解:在△ABC中,∵acosA=bcosB,由正弦定理可得 sinAcosA=sinBcosB,即 $\frac{1}{2}$sin2A=$\frac{1}{2}$sin2B,
∴2A=2B,或 2A+2B=π.
∴A=B,或 A+B=$\frac{π}{2}$,即 C=$\frac{π}{2}$.
故△ABC是等腰三角形或直角三角形,
故选:B.
点评 本题主要考查正弦定理的应用,得到2A=2B,或 2A+2B=π,是解题的关键,属于中档题.

练习册系列答案
相关题目
15.定义运算a?b为执行如右图所示的程序框图输出的S值,则$({2^-}^{{{log}_2}3})?({log_{\frac{1}{2}}}4)$的值为( )
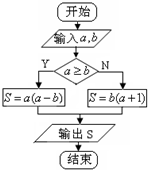

| A. | $\frac{7}{9}$ | B. | $-\frac{8}{3}$ | C. | 4 | D. | -4 |