题目内容
7.函数f(x)=ln(sin2x-cos2x)的定义域是( )| A. | 2kπ-$\frac{3π}{4}$<x<2kπ+$\frac{π}{4}$,k∈Z | B. | 2kπ+$\frac{π}{4}$<x<2k$π+\frac{5π}{4}$,k∈Z | ||
| C. | k$π-\frac{π}{4}$<x<k$π+\frac{π}{4}$,k∈Z | D. | k$π+\frac{π}{4}$<x<k$π+\frac{3π}{4}$,k∈Z |
分析 据对数的真数大于0,列出不等式;结合三角函数的图象求出定义域.
解答 解:要使函数有意义,需使sin2x-cos2x>0,即cos2x<0所以2kπ+$\frac{π}{2}$<2x<2kπ+$\frac{3π}{2}$,
解得:k$π+\frac{π}{4}$<x<k$π+\frac{3π}{4}$,k∈Z.
故选:D.
点评 本题考查对数函数的真数大于0、二倍角公式以及三角不等式的解法.

练习册系列答案
相关题目
2.已知a+$\frac{1}{a}$=3,则a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$等于( )
| A. | 2 | B. | $\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | $±\sqrt{5}$ |
19.已知函数f(x)=2sin(π-x)•cosx-2sin2x+1,若f($\frac{{x}_{0}}{2}$)=$\frac{\sqrt{3}}{3}$,x0∈(-$\frac{π}{4}$,$\frac{π}{4}$),则cos2x0等于( )
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2\sqrt{3}}{9}$ |

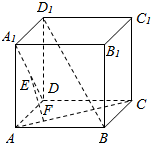 如图,在正方体ABCD-A1B1C1D1中,点E,F分别在A1D,AC上,且EF⊥A1D,EF⊥AC.求证:EF∥BD1.
如图,在正方体ABCD-A1B1C1D1中,点E,F分别在A1D,AC上,且EF⊥A1D,EF⊥AC.求证:EF∥BD1. 如图,四棱锥P-ABCD的底面是边长为a的菱形,平面PCD⊥平面ABCD,PC=a,PD=$\sqrt{2}$a,E为PA的中点,求证:平面EDB⊥平面ABCD.
如图,四棱锥P-ABCD的底面是边长为a的菱形,平面PCD⊥平面ABCD,PC=a,PD=$\sqrt{2}$a,E为PA的中点,求证:平面EDB⊥平面ABCD.