题目内容
8.函数的定义域是$y=(x-1)^{0}+\sqrt{lo{g}_{\frac{2}{3}}(3x-2)}$( )| A. | [$\frac{2}{3},1$] | B. | ($\frac{2}{3},1$] | C. | [$\frac{2}{3},1$) | D. | ($\frac{2}{3},1$) |
分析 由0指数幂的底数不等于0,根式内部的代数式大于等于0联立不等式组得答案.
解答 解:要使原函数有意义,则$\left\{\begin{array}{l}{x-1≠0}\\{lo{g}_{\frac{2}{3}}(3x-2)≥0}\end{array}\right.$,
即$\left\{\begin{array}{l}{x≠1}\\{0<3x-2≤1}\end{array}\right.$,解得$\frac{2}{3}<x<1$.
∴函数$y=(x-1)^{0}+\sqrt{lo{g}_{\frac{2}{3}}(3x-2)}$的定义域是$(\frac{2}{3},1)$.
故选:D.
点评 本题考查函数的定义域及其求法,考查对数不等式的解法,是基础题.

练习册系列答案
相关题目

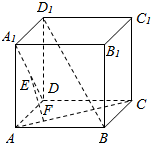 如图,在正方体ABCD-A1B1C1D1中,点E,F分别在A1D,AC上,且EF⊥A1D,EF⊥AC.求证:EF∥BD1.
如图,在正方体ABCD-A1B1C1D1中,点E,F分别在A1D,AC上,且EF⊥A1D,EF⊥AC.求证:EF∥BD1.