题目内容
(本小题满分12分)
如图所示,平面PAD⊥平面ABCD,ABCD为正方形,PA⊥AD,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点。
(1)求证:BC//平面EFG;
(2)求三棱锥E—AFG的体积。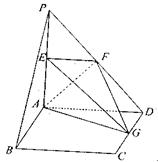
如图所示,平面PAD⊥平面ABCD,ABCD为正方形,PA⊥AD,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点。
(1)求证:BC//平面EFG;
(2)求三棱锥E—AFG的体积。

(1)证明见解析。
(2)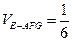
(2)
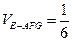
(1)证明: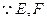 分别是线段PA、PD的中点,
分别是线段PA、PD的中点,
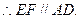 …………2分
…………2分
又∵ABCD为正方形,
∴BC//AD,∴BC//EF。 …………4分
又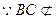 平面EFG,EF
平面EFG,EF 平面EFG,
平面EFG,
∴BC//平面EFG …………6分
(2)∵平面PAD⊥平面ABCD,CD⊥AD,
∴CD⊥平面PAD,即GD⊥平面AEF。 …………8分
又∵EF//AD,PA⊥AD,
∴EF⊥AE。 …………10分
又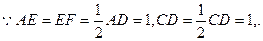
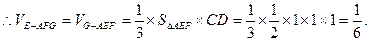 …………12分
…………12分
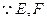 分别是线段PA、PD的中点,
分别是线段PA、PD的中点,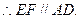 …………2分
…………2分又∵ABCD为正方形,
∴BC//AD,∴BC//EF。 …………4分
又
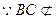 平面EFG,EF
平面EFG,EF 平面EFG,
平面EFG,∴BC//平面EFG …………6分
(2)∵平面PAD⊥平面ABCD,CD⊥AD,
∴CD⊥平面PAD,即GD⊥平面AEF。 …………8分
又∵EF//AD,PA⊥AD,
∴EF⊥AE。 …………10分
又
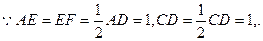
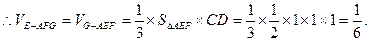 …………12分
…………12分
练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 的三视图如图所示,
的三视图如图所示, ,A1A=
,A1A= ,AB=
,AB= ,AC=2,A1C1=1,
,AC=2,A1C1=1, 在线段
在线段 上且
上且 =
= .
. ⊥平面
⊥平面 ;
; 的余弦值.
的余弦值.
 平面
平面 ,
,
 ,且
,且 ,(1)求证:BE//平面PDA;
,(1)求证:BE//平面PDA; 的中点,求证:
的中点,求证: 平面
平面 ;
; ,求平面PBE与平面ABCD所成的二面角的大小.
,求平面PBE与平面ABCD所成的二面角的大小. 中,底面
中,底面 是边长为2的菱形,且
是边长为2的菱形,且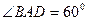 ,
, 为正三角形,
为正三角形, 为
为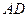 的中点,
的中点, 为棱
为棱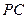 的中点
的中点 平面
平面
 的大小
的大小
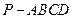 的底面是边长为2的正方形,
的底面是边长为2的正方形,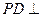
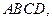
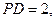
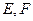 分别为
分别为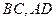 的中点,
的中点,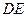 与面
与面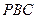 所成角的正弦值;
所成角的正弦值;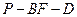 的正切值.
的正切值. 为两条直线,
为两条直线, 为两个平面,下列四个命题中真命题是 ( )
为两个平面,下列四个命题中真命题是 ( ) 所成角相等,则
所成角相等,则



 平面
平面 =
= ,
, ,且
,且 ,二面角
,二面角 .
.  到平面
到平面 的大小为
的大小为 ,求
,求 的值.
的值.
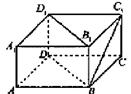
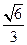
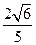
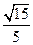
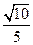
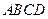 中,
中,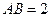 ,
,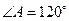 ,沿对角线
,沿对角线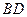 将
将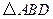 折起,使二面角
折起,使二面角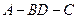 为
为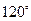 ,则点
,则点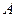 到
到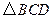 所在平面的距离等于 。
所在平面的距离等于 。