题目内容
【题目】已知函数![]() (
(![]() 是常数).
是常数).
(1)若![]() ,求函数
,求函数![]() 的值域;
的值域;
(2)若![]() 为奇函数,求实数
为奇函数,求实数![]() .并证明
.并证明![]() 的图像始终在
的图像始终在![]() 的图像的下方;
的图像的下方;
(3)设函数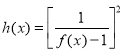 ,若对任意
,若对任意![]() ,以
,以![]() 为边长总可以构成三角形,求
为边长总可以构成三角形,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() ;证明见解析(3)
;证明见解析(3)![]()
【解析】
(1)把![]() 代入后反解可得
代入后反解可得![]() ,解分式不等式即可;
,解分式不等式即可;
(2)直接利用奇函数的定义代入即可求解,利用作差法即可证明结论;
(3)由题意可得![]() ,结合
,结合 ,利用换元法转化为
,利用换元法转化为![]() ,
,![]() ,再结合二次函数的性质即可.
,再结合二次函数的性质即可.
(1)由题意,![]() (
(![]() 是常数),
是常数),
当![]() 时,此时
时,此时![]() ,即
,即![]() ,整理可得
,整理可得![]() ,
,
因![]() ,则
,则![]() ,即
,即![]() ,
,
解得![]() ,
,
故函数![]() 的值域为
的值域为![]() .
.
(2)由题意,![]() 为奇函数,则
为奇函数,则![]() ,即
,即![]() ,
,
化简得![]() ,
,
∵![]() 恒不为零,
恒不为零,
∴![]() 且
且![]() ,解得
,解得![]() ,此时
,此时![]() ,
,
∴![]() ,
,
即![]() 的图像始终在
的图像始终在![]() 的图像的下方.
的图像的下方.
(3)由题意,得![]() ,
, ,
,
令![]() ,则
,则![]() ,其对称轴为
,其对称轴为![]() ,
,
①当![]() ,即
,即![]() 时,此时
时,此时![]() 单调递减,
单调递减,
∴![]() ,即
,即![]() ,
,
解得![]() 或
或![]() ,
,
∴![]() ;
;
②当![]() ,即
,即![]() 时,此时
时,此时![]() 先减后增左端点高,
先减后增左端点高,
∴![]() 即
即![]() ,无解;
,无解;
③当![]() ,即
,即![]() 时,此时
时,此时![]() 先减后增右端点高,
先减后增右端点高,
∴![]() 即
即![]() ,无解;
,无解;
④当![]() ,即
,即![]() 时,此时
时,此时![]() 单调递增,
单调递增,
∴![]() 即
即![]() ,
,
解得![]() 或
或![]() ,
,
∴![]() ;
;
综上,![]() .
.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】假设关于某设备的使用年限x(年)和所支出的维修费用y万元有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图并判断是否线性相关;
(2)如果线性相关,求线性回归方程;
(3)估计使用年限为10年时,维修费用是多少?
附注:①参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]()
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
【题目】某高校在2016年的自主招生考试成绩中随机抽取100位学生的笔试成绩,按成绩分组,得到的频率分布表如下所示.
(1)请先求出频率分布表中①②位置相应的数据,再在答题纸上完成下列频率分布直方图(如图所示);
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| ① | 0.350 |
第3组 |
| 30 | ② |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 | 100 | 1.000 |
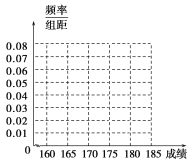
频率分布直方图
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6位学生进入第二轮面试,求第3、4、5组每组各抽取多少位学生进入第二轮面试;
(3)在(2)的前提下,学校决定在6位学生中随机抽取2位学生接受A考官进行面试,求第4组至少有一位学生被考官A面试的概率.