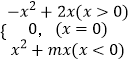题目内容
【题目】已知函数 ![]() 与g(x)=cos(2x+φ)
与g(x)=cos(2x+φ) ![]() ,它们的图象有一个横坐标为
,它们的图象有一个横坐标为 ![]() 的交点.
的交点.
(Ⅰ)求φ的值;
(Ⅱ)将f(x)图象上所有点的横坐标变为原来的 ![]() 倍,得到h(x)的图象,若h(x)的最小正周期为π,求ω的值和h(x)的单调递增区间.
倍,得到h(x)的图象,若h(x)的最小正周期为π,求ω的值和h(x)的单调递增区间.
【答案】解:(Ⅰ)∵函数 ![]() 与g(x)=cos(2x+φ)
与g(x)=cos(2x+φ) ![]() ,它们的图象有一个横坐标为
,它们的图象有一个横坐标为 ![]() 的交点,
的交点,
∴sin ![]() ﹣
﹣ ![]() =cos(
=cos( ![]() +φ),即 cos(
+φ),即 cos( ![]() +φ)=0,∴
+φ)=0,∴ ![]() +φ=
+φ= ![]() ,∴φ=
,∴φ= ![]() .
.
(Ⅱ)将函数 ![]() 的图象上所有点的横坐标变为原来的
的图象上所有点的横坐标变为原来的 ![]() 倍,得到h(x)=sin(ωx)﹣
倍,得到h(x)=sin(ωx)﹣ ![]() 的图象,
的图象,
若h(x)的最小正周期为 ![]() =π,∴ω=2,h(x)=sin(2x)﹣
=π,∴ω=2,h(x)=sin(2x)﹣ ![]() .
.
令2kπ﹣ ![]() ≤2x≤2kπ+
≤2x≤2kπ+ ![]() ,求得kπ﹣
,求得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,可得h(x)的增区间为[kπ﹣
,可得h(x)的增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z.
],k∈Z.
【解析】由题意知f(x)与g(x)的图象有一个横坐标为![]() 的交点,即f(
的交点,即f(![]() )=g(
)=g(![]() ),代入解析式可解得φ的值,(2)根据函数的伸缩变换可得到h(x)的解析式,从而根据正弦函数的图象和性质可得到ω=2和h(x)的单调递增区间.
),代入解析式可解得φ的值,(2)根据函数的伸缩变换可得到h(x)的解析式,从而根据正弦函数的图象和性质可得到ω=2和h(x)的单调递增区间.
【考点精析】通过灵活运用函数y=Asin(ωx+φ)的图象变换,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象即可以解答此题.
的图象即可以解答此题.

【题目】假设某种设备使用的年限x(年)与所支出的维修费用y(元)有以下统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
参考数据: ![]() ,
, ![]() ,
,
如果由资料知y对x呈线性相关关系.试求:
(1)![]() ;
;
(2)线性回归方程 ![]() =bx+a.
=bx+a.
(3)估计使用10年时,维修费用是多少?